题目内容
如图,在三棱柱ABC-A1B1C1中,已知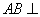 侧面
侧面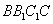 ,AB=BC=1,BB1=2,∠BCC1=
,AB=BC=1,BB1=2,∠BCC1=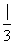 .
.
(1) 求证:C1B⊥平面ABC;
(2)设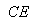 =l
=l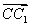 (0≤l≤1),且平面AB1E与BB1E所成的锐二面角
(0≤l≤1),且平面AB1E与BB1E所成的锐二面角
的大小为30°,试求l的值.
解:(1)因为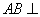 侧面
侧面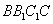 ,
, 侧面
侧面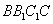 ,故
,故 ,
,
在 中,
中,  由余弦定理得:
由余弦定理得:
 ,
,
所以 , ……3 分
, ……3 分
故 ,所以
,所以 ,而
,而 平面
平面 .……5分
.……5分
(2)由(1)可知, 两两垂直.以
两两垂直.以 为原点,
为原点, 所在直线为
所在直线为
 轴建立空间直角坐标系.
轴建立空间直角坐标系.
则 ,
, ,
, . ……7分
. ……7分
所以 ,所以
,所以 ,
,
则 . 设平面
. 设平面 的法向量为
的法向量为 ,
,
则由 ,得
,得 ,即
,即 ,
,
令 ,则
,则 是平面
是平面 的一个法
的一个法
向量. ……10分
 侧面
侧面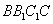 ,
, 是平面
是平面 的一个法向量,
的一个法向量,
 .
.
两边平方并化简得 ,所以
,所以 =1或
=1或 (舍去).…………12分
(舍去).…………12分

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 是虚数,则实数m满足_________________
是虚数,则实数m满足_________________ 满足不等式组
满足不等式组 ,则z=|x|+2
,则z=|x|+2 ,对满足
,对满足 的一切实数
的一切实数 都成立,则实数
都成立,则实数 的取值范围为 .
的取值范围为 .  在点
在点 处的切线方程是( )
处的切线方程是( ) B
B C
C D
D
 ( )
( ) B
B C
C D
D 
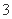 次,一旦发球成功,则停止发球,否则一直发到
次,一旦发球成功,则停止发球,否则一直发到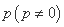 ,发球次数为
,发球次数为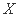 ,若
,若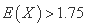 ,则
,则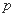 的取值范围是( )
的取值范围是( )
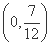

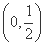

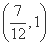


 ”的 ( )
”的 ( )