题目内容
(2007•武汉模拟)已知双曲线y2-x2=1,过上焦点F2的直线与下支交于A、B两点,且线段AF2、BF2的长度分别为m、n.
(1)证明mn≥1;
(2)若m>n,当直线AB的斜率k∈[
,
]时,求
的取值范围.
(1)证明mn≥1;
(2)若m>n,当直线AB的斜率k∈[
| 1 |
| 3 |
| ||
| 5 |
| m |
| n |
分析:(1)双曲线焦点为(0,
).设直线AB的方程为y=kx+
,A(x1,y1),B(x2,y2).k=0时,mn=1.当k≠0时,将y=kx+
代入双曲线方程,消去x得(1-k2)y2-2
y+k2+2=0.由
由双曲线的第二定义,知m=-1+
y1,n=-1+
y2,mn>1.由此可知知mn≥1.
(2)设直线AB的方程为y=kx+
,代入双曲线方程,得(k2-1)x2+2
kx+1=0.由韦达定理知x1+x2=-
,x1•x2=-
.令
=λ,则λ>1,所以
=
,即x1=-λx2.
(1-λ)x2=
,-λ
=
.消去x2,得
=
,由此能求出
的取值范围.
| 2 |
| 2 |
| 2 |
| 2 |
|
| 2 |
| 2 |
(2)设直线AB的方程为y=kx+
| 2 |
| 2 |
2
| ||
| k2-1 |
| 1 |
| k2-1 |
| m |
| n |
| n |
| m |
| x2 |
| -x1 |
(1-λ)x2=
2
| ||
| 1-k2 |
| x | 2 2 |
| 1 |
| k2-1 |
| (1-λ)2 |
| λ |
| 8k2 |
| 1-k2 |
| m |
| n |
解答:解:(1)由题设知双曲线上焦点为(0,
).
设直线AB的方程为y=kx+
,A(x1,y1),B(x2,y2).
当k=0时,A、B两点的横坐标分别为1和-1,
此时mn=1.
当k≠0时,将y=kx+
代入双曲线方程,消去x得(1-k2)y2-2
y+k2+2=0.(2分)由
(4分)
由双曲线的第二定义,知m=-1+
y1,n=-1+
y2(8分)
∴mn=1+2y1y2-
(y1+y2)=
=1+
>1.
综上,知mn≥1.(10分)
(2)设直线AB的方程为y=kx+
,代入双曲线方程,消去y并整理得(k2-1)x2+2
kx+1=0.
∴x1+x2=-
,x1•x2=-
.(8分)
令
=λ,则λ>1,
∴
=
,即x1=-λx2.
∴(1-λ)x2=
,①
-λ
=
.②
由①②,消去x2,得
=
,
即λ+
=
-6③(12分)
由k2∈[
,
],得λ+
∈[3,4],而λ>0,
∴
,解之得
≤λ≤2+
,即为所求.(14分)
| 2 |
设直线AB的方程为y=kx+
| 2 |
当k=0时,A、B两点的横坐标分别为1和-1,
此时mn=1.
当k≠0时,将y=kx+
| 2 |
| 2 |
|
由双曲线的第二定义,知m=-1+
| 2 |
| 2 |
∴mn=1+2y1y2-
| 2 |
| 1+k2 |
| 1-k2 |
| 2 | ||
|
综上,知mn≥1.(10分)
(2)设直线AB的方程为y=kx+
| 2 |
| 2 |
∴x1+x2=-
2
| ||
| k2-1 |
| 1 |
| k2-1 |
令
| m |
| n |
∴
| n |
| m |
| x2 |
| -x1 |
∴(1-λ)x2=
2
| ||
| 1-k2 |
-λ
| x | 2 2 |
| 1 |
| k2-1 |
由①②,消去x2,得
| (1-λ)2 |
| λ |
| 8k2 |
| 1-k2 |
即λ+
| 1 |
| λ |
| 8 |
| 1-k2 |
由k2∈[
| 1 |
| 9 |
| 1 |
| 5 |
| 1 |
| λ |
∴
|
3+
| ||
| 2 |
| 3 |
点评:本题考查直线秘圆锥曲线的综合运用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目
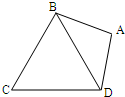 (2007•武汉模拟)如图,在平面四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形,
(2007•武汉模拟)如图,在平面四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形, (2007•武汉模拟)如图,直线l:y=
(2007•武汉模拟)如图,直线l:y=