题目内容
已知全集U=R,非空集合A={x|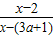 <0},B={x|
<0},B={x|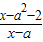 <0}.
<0}.(Ⅰ)当a=
 时,求(∁UB∩A);
时,求(∁UB∩A);(Ⅱ)命题p:x∈A,命题q:x∈B,若q是p的必要条件,求实数a的取值范围.
【答案】分析:(Ⅰ)先求出集合A、B,再求出CUB,借助数轴求出,(CUB)∩A.
(Ⅱ)由题意知,p⇒q,可知A⊆B,B={x|a<x<a2+2}.对于集合A,其解集的端点是 3a+1和2,大小有三种情况,在每种情况下,求出集合A,借助数轴列出A⊆B时区间端点间的大小关系,解不等式组求出a的范围.
解答:解:(Ⅰ)当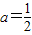 时
时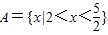 ,
,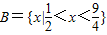 ,(2分)
,(2分)
CUB=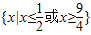 ,(CUB)∩A=
,(CUB)∩A=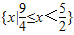 .(4分)
.(4分)
(Ⅱ)由q是p的必要条件,即p⇒q,可知A⊆B.(6分)
由a2+2>a,得 B={x|a<x<a2+2}.(8分)
①当3a+1>2,即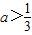 时,A={x|2<x<3a+1},再由
时,A={x|2<x<3a+1},再由 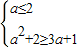 ,解得
,解得 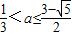 .
.
②当3a+1=2,即a= 时,A=∅,不符合题意;
时,A=∅,不符合题意;
③当3a+1<2,即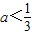 时,A={x|3a+1<x<2},再由
时,A={x|3a+1<x<2},再由 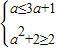 ,解得
,解得 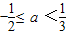 .
.
综上,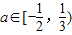 ∪
∪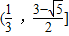 .(12分)
.(12分)
点评:本题考查2个集合间的交、并、补运算方法以及A⊆B时2个区间端点之间的大小关系(借助数轴列出不等关系),
体现了分类讨论的数学思想.
(Ⅱ)由题意知,p⇒q,可知A⊆B,B={x|a<x<a2+2}.对于集合A,其解集的端点是 3a+1和2,大小有三种情况,在每种情况下,求出集合A,借助数轴列出A⊆B时区间端点间的大小关系,解不等式组求出a的范围.
解答:解:(Ⅰ)当
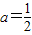 时
时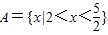 ,
,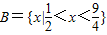 ,(2分)
,(2分)CUB=
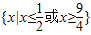 ,(CUB)∩A=
,(CUB)∩A=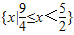 .(4分)
.(4分)(Ⅱ)由q是p的必要条件,即p⇒q,可知A⊆B.(6分)
由a2+2>a,得 B={x|a<x<a2+2}.(8分)
①当3a+1>2,即
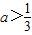 时,A={x|2<x<3a+1},再由
时,A={x|2<x<3a+1},再由 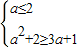 ,解得
,解得 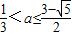 .
.②当3a+1=2,即a=
 时,A=∅,不符合题意;
时,A=∅,不符合题意;③当3a+1<2,即
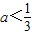 时,A={x|3a+1<x<2},再由
时,A={x|3a+1<x<2},再由 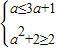 ,解得
,解得 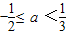 .
.综上,
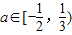 ∪
∪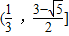 .(12分)
.(12分)点评:本题考查2个集合间的交、并、补运算方法以及A⊆B时2个区间端点之间的大小关系(借助数轴列出不等关系),
体现了分类讨论的数学思想.

练习册系列答案
相关题目
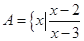 <
<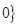 ,
,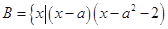 <
<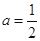 时,求
时,求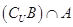 ;
;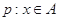 ,命题
,命题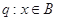 ,若q是p的必要条件,求实数a的取值范围.
,若q是p的必要条件,求实数a的取值范围.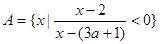 ,
, .
.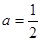 时,求(∁U
时,求(∁U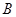 )
)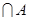 ;
; ,命题
,命题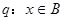 ,若
,若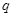 是
是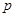 的必要条件,求实数
的必要条件,求实数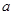 的取值范围
的取值范围