题目内容
已知全集U=R,非空集合A={x|
<0},B={x|
<0}.
(Ⅰ)当a=
时,求(CuB)∩A;
(Ⅱ)命题p:x∈A,命题q:x∈B,若q是p的必要条件,求实数a的取值范围.
| x-2 |
| x-3 |
| x-(a2+2) |
| x-a |
(Ⅰ)当a=
| 1 |
| 2 |
(Ⅱ)命题p:x∈A,命题q:x∈B,若q是p的必要条件,求实数a的取值范围.
分析:(Ⅰ)通过a=
,求出集合B,求出集合A,然后求出集合B的补集,即可求(CuB)∩A;
(Ⅱ)利用q是p的必要条件,说明A⊆B,列出a的关系式,然后求实数a的取值范围.
| 1 |
| 2 |
(Ⅱ)利用q是p的必要条件,说明A⊆B,列出a的关系式,然后求实数a的取值范围.
解答:解:(Ⅰ)A={x|2<x<3},
当a=
时,,B={x|
<x<
},(2分)
?UB={x|x≤
或x≥
},
∴(?UB)∩A={x|
≤x<3}.(4分)
(Ⅱ)由若q是p的必要条件,即p⇒q,可知A⊆B.(6分)
由a2+2>a,B={x|a<x<a2+2} (8分)
∴
,解得a≤-1或1≤a≤2.(12分)
当a=
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 4 |
?UB={x|x≤
| 1 |
| 2 |
| 9 |
| 4 |
∴(?UB)∩A={x|
| 9 |
| 4 |
(Ⅱ)由若q是p的必要条件,即p⇒q,可知A⊆B.(6分)
由a2+2>a,B={x|a<x<a2+2} (8分)
∴
|
点评:本题考查集合的基本运算,充要条件的应用,考查分析问题解决问题的能力.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
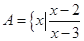 <
<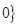 ,
,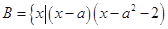 <
<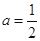 时,求
时,求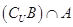 ;
;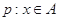 ,命题
,命题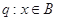 ,若q是p的必要条件,求实数a的取值范围.
,若q是p的必要条件,求实数a的取值范围.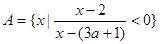 ,
, .
.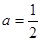 时,求(∁U
时,求(∁U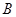 )
)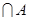 ;
; ,命题
,命题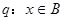 ,若
,若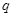 是
是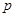 的必要条件,求实数
的必要条件,求实数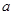 的取值范围
的取值范围