题目内容
已知直线ay-y+2a=0和（2a-1）x+ay+a=0互相垂直，则a=________．
0或1
分析：当a=0 时，其中有一条直线的斜率不存在，经检验满足条件，当a≠0 时，两直线的斜率都存在，
由斜率之积等于-1，可求 a．
解答：当a=0 时，两直线分别为 y=0，和x=0，满足垂直这个条件，
当a≠0 时，两直线的斜率分别为a 和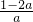
，由斜率之积等于-1得：a•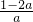=-1，
解得 a=1，综上，a=0 或a=1．
故答案为 0或1．
点评：本题考查两条直线垂直的条件，注意当直线的斜率不存在时，要单独检验，体现了分类讨论的数学思想．
分析：当a=0 时，其中有一条直线的斜率不存在，经检验满足条件，当a≠0 时，两直线的斜率都存在，
由斜率之积等于-1，可求 a．
解答：当a=0 时，两直线分别为 y=0，和x=0，满足垂直这个条件，
当a≠0 时，两直线的斜率分别为a 和
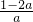，由斜率之积等于-1得：a•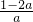=-1，解得 a=1，综上，a=0 或a=1．
故答案为 0或1．
点评：本题考查两条直线垂直的条件，注意当直线的斜率不存在时，要单独检验，体现了分类讨论的数学思想．
练习册系列答案
相关题目
已知直线l1：x+ay+1=0与直线l2：y=
x+2垂直，则a的值是（ ）
| 1 |
| 2 |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|