题目内容
已知直线 L1:2x+ay+6=0和 L2:(a-1)+y+a2-1=0,当a为何值时,两条直线(1)平行、(2)重合、(3)相交、(4)垂直.
分析:直接利用,
(1)两直线ax+by+c=0与mx+ny+d=0平行?
=
≠
(m≠0,n≠0,d≠0);
(2)两直线ax+by+c=0与mx+ny+d=0重合?
=
=
(m≠0,n≠0,d≠0);
(3)两直线ax+by+c=0与mx+ny+d=0相交?
≠
(m≠0,n≠0);
(4)两直线ax+by+c=0与mx+ny+d=0垂直?am+bn=0.求解即可.
(1)两直线ax+by+c=0与mx+ny+d=0平行?
| a |
| m |
| b |
| n |
| c |
| d |
(2)两直线ax+by+c=0与mx+ny+d=0重合?
| a |
| m |
| b |
| n |
| c |
| d |
(3)两直线ax+by+c=0与mx+ny+d=0相交?
| a |
| m |
| b |
| n |
(4)两直线ax+by+c=0与mx+ny+d=0垂直?am+bn=0.求解即可.
解答:解:(1)直线 L1:2x+ay+6=0和 L2:(a-1)+y+a2-1=0,平行
满足
=
≠
,解得a=-1,
所以a=-1时,两条直线平行.
(2)直线 L1:2x+ay+6=0和 L2:(a-1)+y+a2-1=0,重合,
满足
=
=
,解得a=2,
所以a=2时两条直线重合.
(3)直线 L1:2x+ay+6=0和 L2:(a-1)+y+a2-1=0,相交,
满足
≠
,解得a≠-1,a≠2.
所以a≠-1,a≠2.时两条直线相交.
(4)直线 L1:2x+ay+6=0和 L2:(a-1)+y+a2-1=0,垂直,
满足2×(a-1)+a×1=0,解得a=
,
所以a=
时,两条直线垂直.
满足
| 2 |
| a-1 |
| a |
| 1 |
| 6 |
| a2-1 |
所以a=-1时,两条直线平行.
(2)直线 L1:2x+ay+6=0和 L2:(a-1)+y+a2-1=0,重合,
满足
| 2 |
| a-1 |
| a |
| 1 |
| 6 |
| a2-1 |
所以a=2时两条直线重合.
(3)直线 L1:2x+ay+6=0和 L2:(a-1)+y+a2-1=0,相交,
满足
| 2 |
| a-1 |
| a |
| 1 |
所以a≠-1,a≠2.时两条直线相交.
(4)直线 L1:2x+ay+6=0和 L2:(a-1)+y+a2-1=0,垂直,
满足2×(a-1)+a×1=0,解得a=
| 2 |
| 3 |
所以a=
| 2 |
| 3 |
点评:本题考查两条直线的位置关系,用好直线的位置关系是解题的关键,考查计算能力.

练习册系列答案
相关题目
已知直线l1:2x-my+1=0与l2:x+(m-1)y-1=0,则“m=2”是“l1⊥l2”的( )
| A、充分不必要条件 | B、必要不充分条件 | C、充分且必要条件 | D、既不充分又不必要条件 |
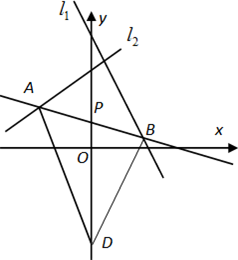 如图,直线L过点P(0,1),夹在两已知直线l1:2x+y-8=0和l2:x-3y+10=0之间的线段AB恰被点P平分.
如图,直线L过点P(0,1),夹在两已知直线l1:2x+y-8=0和l2:x-3y+10=0之间的线段AB恰被点P平分.