题目内容
已知过抛物线y2=2px（p＞0）焦点的弦长为
p.求弦所在直线的方程.
思路解析：设出斜率k,利用韦达定理求解或设出直线的倾斜角,利用|AB|= 解法一：设焦点F( 若|AB|⊥Ox，则|AB|=2p＜ 由 ∴y1+y2= ∴|AB|= 解之，得k=±2，∴弦所在直线方程为y=2（x- 解法二：设弦AB所在直线的倾斜角为θ，则|AB|= ∴sin2θ= ∴弦所在直线方程为y=2（x-
求解.
,0).A、B为弦的两端点，坐标为A（x1，y1）、B（x2，y2）.
p.∴直线AB斜率存在,设为k.
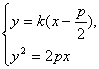消去x,整理得ky2-2py-kp2=0,
,y1y2=-p2.
·
=2p·（1+
）=
p.
）或y=-2（x-
）.
=
p.
.∴cos2θ=
，tan2θ=4.∴kAB=tanθ=±2.
），或y=-2（x-
）.
练习册系列答案
同步拓展与训练系列答案
升级创优卷系列答案
一课3练三好练习系列答案
金版卷王名师面对面期末大冲刺系列答案
大阅读周周练系列答案
高分拔尖提优教程系列答案
培优闯关NO1期末冲刺卷系列答案
全解全习课时达标讲练测系列答案
完全大考卷冲刺名校系列答案
实验探究与指导系列答案
相关题目
．