题目内容

13、已知过抛物线y2=4x的焦点F的直线交该抛物线于A、B两点，|AF|=2，则|BF|=
2
．
．
分析：抛物线上任一点到焦点的距离与到准线的距离是相等的．已知|AF|=2，则到准线的距离也为2，根据图形AFKA1是正方形．
则易得AB⊥x轴，即可得答案．
解答：解：由抛物线的定义．抛物线上任一点到焦点的距离与到准线的距离是相等的．
已知|AF|=2，则到准线的距离也为2．根据图形AFKA1，是正方形．
可知|AF|=|AA1|=|KF|=2∴AB⊥x轴故|AF|=|BF|=2．
故填|BF|=2．
点评：活用圆锥曲线的定义是解决圆锥曲线最基本的方法．到焦点的距离，叫焦半径．到焦点的距离常转化到准线的距离求解．
练习册系列答案
相关题目
（文科做（1）（2）（4），理科全做）
已知过抛物线C1：y2=2px（p＞0）焦点F的直线交抛物线于A（x1，y1），B（x2，y2）两点 
（1）证明：y1y2=-p2且（y1+y2）2=2p（x1+x2-p）；
（2）点Q为线段AB的中点，求点Q的轨迹方程；
（3）若x1=1，x2=4，以坐标轴为对称轴的椭圆或双曲线C2过A、B两点，求曲线C1和C2的方程；
（4）在（3）的条件下，若曲线C2的两焦点分别为F1、F2，线段AB上有两点C（x3，y3），D（x4，y4）（x3＜x4），满足：①S△F1F2A-S△F1F2C=S△F1F2D-S△F1F2B，②AB=3CD．在线段F1 F2上是否存在一点P，使PD=
11
，若存在，求出点P的坐标；若不存在，说明理由．
已知以抛物线y2=4x过焦点的弦为直径且圆心在第四象限的圆截y轴所得弦长为4，那么该圆的方程是
（x-
3
2
）2+（y+1）2=
25
4
（x-
3
2
）2+（y+1）2=
25
4
．
（理）已知过抛物线y2=6x焦点的弦长为12，则此弦所在直线的倾斜角是（　　）
已知过抛物线y2=4x焦点F的直线l与抛物线相交于A，B两点，若|AF|=4，则|BF|=
 
．

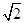已知过抛物线y2 =2px（p>0）的焦点F的直线x－my+m=0与抛物线交于A，B两点，且△OAB（O为坐标原点）的面积为2，则m6+ m4的值为（   ）

A．1                B． 2               C．3                D．4

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网