题目内容
斜率为1的直线l与椭圆
+y2=1相交于A,B两点,则|AB|得最大值为 .
| x2 |
| 4 |
考点:直线与圆锥曲线的综合问题,椭圆的应用
专题:圆锥曲线的定义、性质与方程
分析:设出直线的方程,代入椭圆方程中消去y,根据判别式大于0求得t的范围,进而利用弦长公式求得|AB|的表达式,利用t的范围求得|AB|的最大值.
解答:
解:设直线l的方程为y=x+t,代入椭圆
+y2=1消去y得
x2+2tx+t2-1=0,
由题意得△=(2t)2-5(t2-1)>0,即t2<5.
弦长|AB|=4
×
≤
.当t=0时取最大值.
故答案为:
.
| x2 |
| 4 |
| 5 |
| 4 |
由题意得△=(2t)2-5(t2-1)>0,即t2<5.
弦长|AB|=4
| 2 |
| ||
| 5 |
4
| ||
| 5 |
故答案为:
4
| ||
| 5 |
点评:本题主要考查了椭圆的应用,直线与椭圆的关系.常需要把直线与椭圆方程联立,利用韦达定理,判别式找到解决问题的突破口.

练习册系列答案
相关题目
为了得到y=cos(2x+
)函数的图象,只需将余弦函数曲线上所有的点( )
| 1 |
| 3 |
A、先向右平移
| ||||
B、先向左平移
| ||||
C、先向左平移
| ||||
D、先向右平移
|
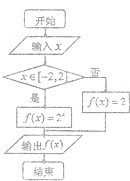 阅读如图所示的程序框图,如果输出的函数值在区间[
阅读如图所示的程序框图,如果输出的函数值在区间[| 1 |
| 4 |
| 1 |
| 2 |
| A、(-∞,-2) |
| B、[-2,-1] |
| C、[-1,2] |
| D、(2,+∞) |
某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点.为调查产品的销售情况,现进行两种调查:①从这600个销售点中抽取一个容量为100的样本;②在丙地区中有20个特大型销售点,要从中抽取7个调查其销售收入和售后服务情况,则完成①、②这两项调查宜采用的抽样方法依次是( )
| A、分层抽样法,系统抽样法 |
| B、分层抽样法,简单随机抽样法 |
| C、系统抽样法,分层抽样法 |
| D、简单随机抽样法,分层抽样法 |
在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,已知bcosB=acosA,则△ABC的形状是( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等腰三角形或直角三角形 |
在等比数列{an}中,a2a3a7=8,则a4=( )
| A、1 | ||
| B、4 | ||
| C、2 | ||
D、2
|