题目内容
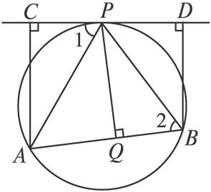
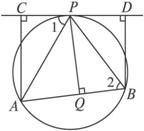
如图,AB为⊙O的弦,CD切⊙O于P,AC⊥CD于C,BD⊥DC于D,PQ⊥AB于Q,求证:PQ2=AC·BD.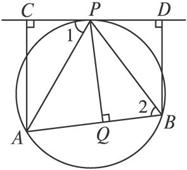
思路点拨:欲证PQ2=AC·BD,只需证明AC∶PQ=PQ∶BD,图中没有产生比例中项的条件,需要通过过渡比来解决.连结PA、PB,利用弦切角定理,得到不相邻的两对直角三角形分别相似.
证明:连结PA、PB,如图所示.

∵CD切⊙O于P,∴∠1=∠2.
∵AC⊥CD于C,PQ⊥AB于Q,
∴∠ACP=∠PQB=90°.
∴△ACP∽△PQB.
∴AC∶PQ=AP∶BP.
同理,△BDP∽△PQA,
∴PQ∶BD=AP∶BP.
∴AC∶PQ=PQ∶BD,
即PQ2=AC·BD.
[一通百通]弦切角是沟通圆内已知和未知的桥梁,它在解决圆内有关等角问题中可以大显身手.利用弦切角定理解题能够锻炼我们思维的广阔性和深刻性,希望同学们在解题时灵活运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

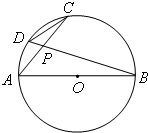 (2007•深圳一模)请从下面两题中选做一题,如果两题都做,以第一题的得分为最后得分.
(2007•深圳一模)请从下面两题中选做一题,如果两题都做,以第一题的得分为最后得分.