题目内容
设a、b、c 为△ABC 的三边,求证:方程x2+2ax+b2=0 与x2+2cx-b2=0 有公共根的充要条件是A=90 °
证明:
充分性:
∵A=90 °,∴a2=b2+c2 ,
于是方程x2+2ax+b2=0 可化为x2+2ax+a2-c2=0.
∴x2+2ax+(a+c)(a-c)=0,
∴[x+(a+c)][x+(a-c)]=0 ,
∴该方程有两个根x1=-(a+c) ,x2=-(a-c).
同理,另一方程x2+2cx-b2=0 可化为x2+2ex-(a2-e2)=0 ,
∴x2+2cx+(c+a)(c-a)=0 ,
∴[x+(c+a)][x+(c-a)]=0,
∴该方程有两个根x3=-(a+c) ,x4=-(c-a ).可以发现x1=x3 ,
∴这两个方程有公共根,
必要性:
设α是两方程的公共根,

由①+②得2α2+2α(a+c) =0.
∵α≠0
∴α=-(a+c),
将α=-(a+c)代入①得a2=b2+c2.
∴A=90°.
综上可知,方程x2+2ax+b2=0与x2+2cx-b2=0有公共根的充要条件是A=90°
充分性:
∵A=90 °,∴a2=b2+c2 ,
于是方程x2+2ax+b2=0 可化为x2+2ax+a2-c2=0.
∴x2+2ax+(a+c)(a-c)=0,
∴[x+(a+c)][x+(a-c)]=0 ,
∴该方程有两个根x1=-(a+c) ,x2=-(a-c).
同理,另一方程x2+2cx-b2=0 可化为x2+2ex-(a2-e2)=0 ,
∴x2+2cx+(c+a)(c-a)=0 ,
∴[x+(c+a)][x+(c-a)]=0,
∴该方程有两个根x3=-(a+c) ,x4=-(c-a ).可以发现x1=x3 ,
∴这两个方程有公共根,
必要性:
设α是两方程的公共根,

由①+②得2α2+2α(a+c) =0.
∵α≠0
∴α=-(a+c),
将α=-(a+c)代入①得a2=b2+c2.
∴A=90°.
综上可知,方程x2+2ax+b2=0与x2+2cx-b2=0有公共根的充要条件是A=90°

练习册系列答案
相关题目

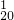 +C
+C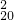 •2+C
•2+C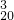 •22+…+C
•22+…+C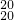 •219,b≡a(mon 10),则b的值可以是
•219,b≡a(mon 10),则b的值可以是