题目内容
设a、b、m为整数(m>0),若a和b被m除得的余数相同,则称a和b对模m 同余.记为a≡b(mod m).已知a=2+C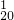 +C
+C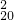 •2+C
•2+C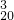 •22+…+C
•22+…+C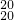 •219,b≡a(mon 10),则b的值可以是
•219,b≡a(mon 10),则b的值可以是
- A.2015
- B.2012
- C.2008
- D.2006
B
分析:根据已知中a和b对模m同余的定义,结合二项式定理,我们可以求出a的值,结合a≡b(bmod10),比较四个答案中的数字,结合得到答案.
解答:∵已知a=2+ +
+ •2+
•2+ •22 +…+
•22 +…+ •219
•219
= (
( +
+ •2+
•2+ •22+
•22+ •23+…+
•23+…+ •220 )+
•220 )+
= •(1+2)20+
•(1+2)20+ =
= •320+
•320+ ,
,
∵31个位是3,32个位是9,33个位是7,34个位是1,35个位是3,…
∴320个位是1,故a= •320+
•320+ 的个位数是2.
的个位数是2.
又∵b≡a(bmod10),
∴b的个位也是2,结合所给的选项,
故选B.
点评:本题考查的知识点是同余定理,其中正确理解a和b对模m同余,是解答本题的关键,同时利用二项式定理求出a的值,也很关键,属于中档题.
分析:根据已知中a和b对模m同余的定义,结合二项式定理,我们可以求出a的值,结合a≡b(bmod10),比较四个答案中的数字,结合得到答案.
解答:∵已知a=2+
 +
+ •2+
•2+ •22 +…+
•22 +…+ •219
•219 =
 (
( +
+ •2+
•2+ •22+
•22+ •23+…+
•23+…+ •220 )+
•220 )+
=
 •(1+2)20+
•(1+2)20+ =
= •320+
•320+ ,
,∵31个位是3,32个位是9,33个位是7,34个位是1,35个位是3,…
∴320个位是1,故a=
 •320+
•320+ 的个位数是2.
的个位数是2.又∵b≡a(bmod10),
∴b的个位也是2,结合所给的选项,
故选B.
点评:本题考查的知识点是同余定理,其中正确理解a和b对模m同余,是解答本题的关键,同时利用二项式定理求出a的值,也很关键,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目