题目内容
【题目】如果函数f(x)=3sin(2x+φ)的图象关于点( ![]() ,0)成中心对称(|φ|<
,0)成中心对称(|φ|< ![]() ),那么函数f(x)图象的一条对称轴是( )
),那么函数f(x)图象的一条对称轴是( )
A.x=﹣ ![]()
B.x= ![]()
C.x= ![]()
D.x= ![]()
【答案】B
【解析】解:∵函数f(x)=3sin(2x+φ)的图象关于点( ![]() ,0)成中心对称, ∴2×
,0)成中心对称, ∴2× ![]() +φ=kπ,k∈Z,解得:φ=kπ﹣
+φ=kπ,k∈Z,解得:φ=kπ﹣ ![]() ,k∈Z,
,k∈Z,
∵|φ|< ![]() ,
,
∴φ= ![]() ,可得:f(x)=3sin(2x+
,可得:f(x)=3sin(2x+ ![]() ),
),
∴令2x+ ![]() =kπ+
=kπ+ ![]() ,k∈Z,可得:x=
,k∈Z,可得:x= ![]() +
+ ![]() ,k∈Z,
,k∈Z,
∴当k=0时,可得函数的对称轴为x= ![]() .
.
故选:B.
由正弦函数的对称性可得2× ![]() +φ=kπ,k∈Z,结合范围|φ|<
+φ=kπ,k∈Z,结合范围|φ|< ![]() ,可求φ,令2x+
,可求φ,令2x+ ![]() =kπ+
=kπ+ ![]() ,k∈Z,可求函数的对称轴方程,对比选项即可得解.
,k∈Z,可求函数的对称轴方程,对比选项即可得解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 50 | 60 | 70 |
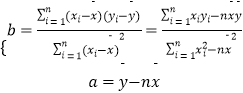
(1)画出散点图;
(2)求线性回归方程;
(3)预测当广告费支出为7百万元时的销售额.参考公式:.