题目内容
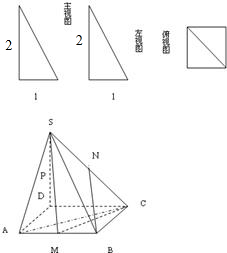
 一个多面体的三视图(正视图、侧视图、俯视图)如图所示,M,N分别是B1C1,A1B的中点.
一个多面体的三视图(正视图、侧视图、俯视图)如图所示,M,N分别是B1C1,A1B的中点.(1)求证:MN∥平面ACC1A1;
(2)求证:MN⊥平面A1BC;
(3)若这个多面体的六个顶点A,B,C,A1,B1,C1都在同一个球面上,求这个球的体积.
分析:(1)根据三视图的性质,可得该几何体是直三棱柱,且AC⊥BC,AC=BC=CC1.连接AC1,AB1,矩形ABB1A1中对角线AB1的中点N就是A1B的中点.结合M是B1C1的中点证出MN∥AC1,由线面平行的判定定理,证出MN∥平面ACC1A1.
(2)由BC⊥平面ACC1A1,得到BC⊥AC1.正方形ACC1A1中可得A1C⊥AC1,结合线面垂直判定定理,证出AC1⊥平面A1BC,再由MN∥AC1,可得MN⊥平面A1BC;
(3)根据三棱柱ABC-A1B1C1是直三棱柱,在矩形ABB1A1中算出可得A1B=
a,从而得到NA=NB=NA1=
a,同理得NC=NB1=NC1=
a,所以点N是多面体的外接球心,得到半径R=
a.由球的体积公式,即可算出该外接球的体积.
(2)由BC⊥平面ACC1A1,得到BC⊥AC1.正方形ACC1A1中可得A1C⊥AC1,结合线面垂直判定定理,证出AC1⊥平面A1BC,再由MN∥AC1,可得MN⊥平面A1BC;
(3)根据三棱柱ABC-A1B1C1是直三棱柱,在矩形ABB1A1中算出可得A1B=
| 3 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
解答: 解:由题意可知,这个几何体是直三棱柱,且AC⊥BC,AC=BC=CC1,
解:由题意可知,这个几何体是直三棱柱,且AC⊥BC,AC=BC=CC1,
(Ⅰ)连接AC1,AB1,由直三棱柱的性质,得AA1⊥平面A1B1C1,
∴AA1⊥A1B1,可得四边形ABB1A1为矩形.
由矩形的性质,得AB1过A1B的中点N.
在AB1C1中,由中位线性质得MN∥AC1,
又∵AC1?平面ACC1A1MN?平面ACC1A1,∴MN∥平面ACC1A1.…(4分)
(Ⅱ)∵BC⊥平面ACC1A1,AC1?平面ACC1A1,∴BC⊥AC1
在正方形ACC1A1中,可得A1C⊥AC1
又∵BC∩A1C=C,∴AC1⊥平面A1BC
又∵MN∥AC1,∴MN⊥平面A1BC…(8分)
(Ⅲ)∵多面体为直三棱柱,
∴矩形ABB1A1中,A1B2=AA12+AB2=a2+(
a)2=3a2
可得A1B=
a,
∵AN是直角三角形斜边的中线,∴NA=NB=NA1=
a
同理可得NC=NB1=NC1=
a
∴N是这个多面体的外接球的球心,半径R=
a…(10分)
∴外接球的体积V=
π(
a)3=
πa3…(14分)
 解:由题意可知,这个几何体是直三棱柱,且AC⊥BC,AC=BC=CC1,
解:由题意可知,这个几何体是直三棱柱,且AC⊥BC,AC=BC=CC1,(Ⅰ)连接AC1,AB1,由直三棱柱的性质,得AA1⊥平面A1B1C1,
∴AA1⊥A1B1,可得四边形ABB1A1为矩形.
由矩形的性质,得AB1过A1B的中点N.
在AB1C1中,由中位线性质得MN∥AC1,
又∵AC1?平面ACC1A1MN?平面ACC1A1,∴MN∥平面ACC1A1.…(4分)
(Ⅱ)∵BC⊥平面ACC1A1,AC1?平面ACC1A1,∴BC⊥AC1
在正方形ACC1A1中,可得A1C⊥AC1
又∵BC∩A1C=C,∴AC1⊥平面A1BC
又∵MN∥AC1,∴MN⊥平面A1BC…(8分)
(Ⅲ)∵多面体为直三棱柱,
∴矩形ABB1A1中,A1B2=AA12+AB2=a2+(
| 2 |
可得A1B=
| 3 |
∵AN是直角三角形斜边的中线,∴NA=NB=NA1=
| ||
| 2 |
同理可得NC=NB1=NC1=
| ||
| 2 |
∴N是这个多面体的外接球的球心,半径R=
| ||
| 2 |
∴外接球的体积V=
| 4 |
| 3 |
| ||
| 2 |
| ||
| 2 |
点评:本题给出直三棱柱的三视图,求证线面平行、线面垂直并求外接球的体积.着重考查了三角形中位线定理、线面平行垂直的判定与性质和球的体积公式等知识,属于中档题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
如图是一个多面体的三视图,则其全面积为( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 已知一个多面体的三视图如图所示,则这个多面体的体积等于
已知一个多面体的三视图如图所示,则这个多面体的体积等于 一个多面体的三视图如图所示,其中正视图是正方形,侧视图是等腰三角形.则该几何体的体积为( )
一个多面体的三视图如图所示,其中正视图是正方形,侧视图是等腰三角形.则该几何体的体积为( ) (2010•台州一模)一个多面体的三视图分别是正方形、等腰三角形和矩形,其尺寸如图,则该多面体的体积为( )
(2010•台州一模)一个多面体的三视图分别是正方形、等腰三角形和矩形,其尺寸如图,则该多面体的体积为( )