题目内容
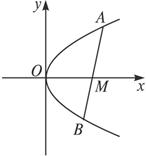
如图所示,线段AB过x轴正半轴上一点M(m,0)(m>0),端点A、B到x轴的距离之积为2m,以x轴为对称轴,过A、O、B三点作抛物线.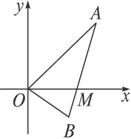
(1)求此抛物线方程;
(2)若tan∠AOB=-1,求m的取值范围.
解:(1)当AB不垂直于x轴时,设AB方程为y=k(x-m),抛物线方程为y2=2px(p>0).
由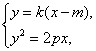 得ky2-2py-2pkm=0,
得ky2-2py-2pkm=0,
∴y1y2=-2pm.∴|y1y2|=2pm=2m.
∴p=1.当AB⊥x轴时,A、B分别为(m,![]() )、(m,-
)、(m,-![]() ),由题意有2pm=2m,p=1,故所求抛物线方程为y2=2x.
),由题意有2pm=2m,p=1,故所求抛物线方程为y2=2x.
(2)设A(![]() ,y1),B(
,y1),B(![]() ,y2),
,y2),
由(1)知y1y2=-2m,y1+y2=![]() ,
,
∴|y1-y2|=![]()
=![]() .又tan∠AOB=-1,
.又tan∠AOB=-1,
k1=![]() ,k2=
,k2=![]() ,
,
∴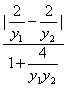 =-1,即y1y2+4=2|y1-y2|.
=-1,即y1y2+4=2|y1-y2|.
∴-2m+4=2![]() .①
.①
平方后化简,得m2-12m+4=![]() .
.
∴m2-12m+4>0.
∴m<6-4![]() 或m>6+4
或m>6+4![]() .
.
又由①知-2m+4>0,∴m<2.
∴m的取值范围为0<m<6-4![]() 且AB⊥x轴时,
且AB⊥x轴时,
y1=2(![]() -1),y2=-2(
-1),y2=-2(![]() -1),y1y2=-4(
-1),y1y2=-4(![]() -1)2=-2m,tan∠AOB=-1符合条件.
-1)2=-2m,tan∠AOB=-1符合条件.
故符合条件的m的取值范围为0<m≤6-4![]() .
.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
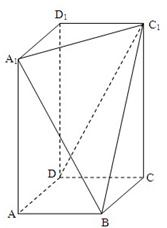 在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后.得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为
在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后.得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为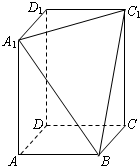 在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后,得如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为
在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后,得如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为