题目内容
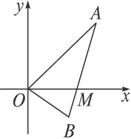
如图所示,线段AB过x轴正半轴上一定点M(m,0),端点A、B到x轴的距离之积为2m,以x轴为对称轴,过A、O、B三点作抛物线.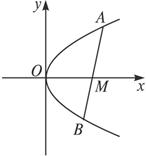
(1)求抛物线的方程;
(2)若tan∠AOB=-1,求m的取值范围.
解:(1)设所求抛物线方程为y2=2px(p>0),直线AB的方程为x=ky+m.
代入y2=2px,得y2-2pky-2pm=0.则yayb=-2pm=-2m.
∴p=1.抛物线方程为y2=2x.
(2)设A(x1,y1)、B(x2,y2),把x=ky+m代入y2=2x,得y2-2ky-2m=0.
∴y1+y2=2k,y1y2=-2m.
又y12=2x1,y22=2x2,
∴kOA=![]() ,kOB=
,kOB=![]() .
.
∵tan∠AOB=-1,
∴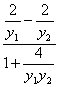 =-1.
=-1.
∴y1y2+4=2(y1-y2),
即-2m+4=2![]() .
.
∴m2-12m+4=4k2≥0,0<m≤2.
∴0<m≤6-4![]() .
.

练习册系列答案
相关题目
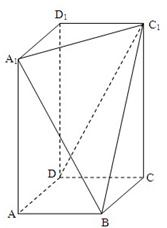 在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后.得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为
在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后.得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为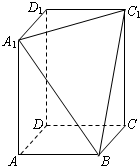 在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后,得如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为
在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后,得如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为