Question

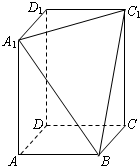在长方体ABCD-A₁B₁C₁D₁中，AB=BC=2，过A₁，C₁，B三点的平面截去长方体的一个角后，得如图所示的几何体ABCD-A₁C₁D₁，且这个几何体的体积为

40

3

．
（1）求棱A₁A的长；
（2）若在线段BC₁上存在点P，使直线A₁P⊥C₁D，求二面角D-A₁P-B的大小．

Answer 1

分析：（1）利用V_ABCD-A1C1D1=VABCD-A1B1C1D1-VB-A1BC1，建立方程，即可求得A₁A的长；
（2）以

DA

，

DC

，

DD1

为x轴、y轴、z轴建立空间直角坐标系，利用A₁P⊥C₁D，求出点P的坐标，进而可求平面DA₁P 的法向量

m

=（（2，1，-1），平面BA₁P的法向量

n

=（2，2，1），利用向量的夹角公式，即可求得二面角D-A₁P-B的大小．

解答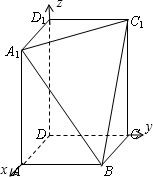：解：（1）设A₁A=h，则V_ABCD-A1C1D1=VABCD-A1B1C1D1-VB-A1BC1=2×2×h-

1

3

×

1

2

×2×2×h=

40

3

解得：h=4，即A₁A的长为4．（4分）
（2）以

DA

，

DC

，

DD1

为x轴、y轴、z轴建立空间直角坐标系，则A₁（2，0，4），B（2，2，0），C₁（0，2，4）（6分）

BC1

=(-2，0，4)，

BP

=(x-2，0，z)
若在线段BC₁上存在点P（x，2，z）（0≤x≤2，0≤z≤4）使直线A₁P⊥C₁D
∵P、B、C₁共线，∴

x-2

-2

=

z

4

，∴z=4-2x
∴

A1P

=(x-2，2，-2x)
由A₁P⊥C₁D得：（x-2，2，-2x）•（0，2，4）=0，解得：x=

1

2

      （8分）
此时点P的坐标为（

1

2

，2，3），
设平面DA₁P 的法向量为

m

=（x，y，z），∴

m • DA1 =0 m • A1P =0

，∴

2x+4z=0 - 3 2 x+2y-z=0

所以可取

m

=（（2，1，-1），
设平面BA₁P的法向量为

n

=（x′，y′，z′），∴

m • BA1 =0 m • A1P =0

，∴

-2y′+4z′=0 - 3 2 x′+2y′-z′=0

所以可取

n

=（2，2，1）（10分）
∴二面角D-A₁P-B的余弦值为

4+2-1

6 ×3

=

5 6

18

∴二面角D-A₁P-B的大小为arccos

5 6

18

（12分）

点评：本题考查几何体轭体积，空间角的计算等基本知识，考查空间想象能力、逻辑思维能力、运算求解能力和探究能力，同时考查学生灵活利用图形，借助向量工具解决问题的能力．