题目内容
如图，点A、B、C都在幂函数
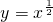的图象上，它们的横坐标分别是a、a+1、a+2又A、B、C在x轴上的射影分别是A′、B′、C′，记△AB′C的面积为f（a），△A′BC′的面积为g（a）
（1）求函数f（a）和g（a）的表达式；
（2）比较f（a）与g（a）的大小，并证明你的结论
解：（1）连接AA′、BB′、CC′，
则f（a）=S△AB'C =S梯形AA'C'C -S△AA'B'-S△CC'B'
=
=
=
（
），
g（a）=S△A′BC′= AC•BB′=BB′=
，
=
=
，
∴f（a）＜g（a），
分析：（1）间接法求f（a），利用f（a）=S△AB'C =S梯形AA'C'C -S△AA'B'-S△CC'B'求出f（a）的值，直接法求g（a）= AC•BB′．
（2）比较f（a）与g（a）的大小，用作差法，化简f（a）-g（a）到因式乘积的形式，判断符号，从而比较大小．
点评：本题考查幂函数的应用，不等式比较大小的方法，体现转化的数学思想．
则f（a）=S△AB'C =S梯形AA'C'C -S△AA'B'-S△CC'B'
=
==（），g（a）=S△A′BC′=
AC•BB′=BB′=， =
=，∴f（a）＜g（a），
分析：（1）间接法求f（a），利用f（a）=S△AB'C =S梯形AA'C'C -S△AA'B'-S△CC'B'求出f（a）的值，直接法求g（a）=
AC•BB′．（2）比较f（a）与g（a）的大小，用作差法，化简f（a）-g（a）到因式乘积的形式，判断符号，从而比较大小．
点评：本题考查幂函数的应用，不等式比较大小的方法，体现转化的数学思想．
练习册系列答案
相关题目
如图，点A、B、C都在幂函数
（2013•蓟县一模）（几何证明选讲）如图，点A、B、C都在⊙O上，过点C的切线交AB的延长线于点D，若AB=5，BC=3，CD=6，则线段AC的长为
（2013•湛江二模）（几何证明选讲选做题）
的图像上，它们的横坐标分别是a、a+1、a+2
又A、B、C在x轴上的射影分别是A′、B′、C′,记△AB′C的面积为f(a),△A′BC′的面积为g(a). 
（几何证明选讲）如图，点A、B、C都在⊙O上，过点C的切线交AB的延长线于点D，若AB=5，BC=3，CD=6，则线段AC的长为 ．