题目内容
 如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=lnx+f′(x)的零点所在的区间是( )
如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=lnx+f′(x)的零点所在的区间是( )分析:由二次函数图象的对称轴确定b的范围,据g(x)的表达式计算g(
)和g(1)的值的符号,从而确定零点所在的区间.
| 1 |
| 2 |
解答:解:∵f(x)=x2-bx+a,结合函数的图象可知,二次函数的对称轴,
<x=
<1
∴1<b<2
∴f’(x)=2x-b
∴g(x)=lnx+f′(x)=lnx+2x-b在(0,+∞)上单调递增且连续
∵g(
)=ln
+1-b<0,g(1)=ln1+2-b=2-b>0,
∴函数g(x)=lnx+f′(x)的零点所在的区间是(
,1)
故选C
| 1 |
| 2 |
| b |
| 2 |
∴1<b<2
∴f’(x)=2x-b
∴g(x)=lnx+f′(x)=lnx+2x-b在(0,+∞)上单调递增且连续
∵g(
| 1 |
| 2 |
| 1 |
| 2 |
∴函数g(x)=lnx+f′(x)的零点所在的区间是(
| 1 |
| 2 |
故选C
点评:本题考查导数的运算、函数零点的判定定理的应用,解题的关键是确定b的范围.

练习册系列答案
相关题目
 如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=lnx+f′(x)的零点所在的区间是
如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=lnx+f′(x)的零点所在的区间是 如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=ex+f′(x)的零点所在的区间是( )
如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=ex+f′(x)的零点所在的区间是( )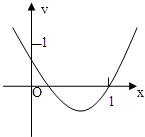 (2012•黄州区模拟)如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=2lnx+f(x)在点(b,g(b))处切线的斜率的最小值是( )
(2012•黄州区模拟)如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=2lnx+f(x)在点(b,g(b))处切线的斜率的最小值是( )

