题目内容
 如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=ex+f′(x)的零点所在的区间是( )
如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=ex+f′(x)的零点所在的区间是( )分析:由图象可知,0<f(0)=a<1,f(1)=0,从而可得b的范围,然后根据零点判定定理可得结论.
解答:解:由图象可知,0<f(0)=a<1①,f(1)=0,即1-b+a=0②,
由①②可得1<b<2,
g(x)=ex+2x-b,且g(0)=1-b<0,g(1)=e+2-b>0,
又g(x)的图象连续不断,所以g(x)在(0,1)上必存在零点,
故选B.
由①②可得1<b<2,
g(x)=ex+2x-b,且g(0)=1-b<0,g(1)=e+2-b>0,
又g(x)的图象连续不断,所以g(x)在(0,1)上必存在零点,
故选B.
点评:本题考查导数的运算、函数零点的判定定理,考查数形结合思想,属中档题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=lnx+f′(x)的零点所在的区间是
如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=lnx+f′(x)的零点所在的区间是 如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=lnx+f′(x)的零点所在的区间是( )
如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=lnx+f′(x)的零点所在的区间是( )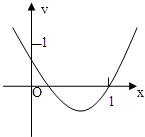 (2012•黄州区模拟)如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=2lnx+f(x)在点(b,g(b))处切线的斜率的最小值是( )
(2012•黄州区模拟)如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=2lnx+f(x)在点(b,g(b))处切线的斜率的最小值是( )

