已知f(x)在R上单调递增.且满足f(-x)=-f(x),若x+y>0,则f(x)+f(y)的符号是否确定?反过来.若f(x)+f(y)>0,则x+y是否一定大于零? 题目和参考答案——青夏教育精英家教网—

题目内容

已知f(x)在R上单调递增，且满足f(－x)=－f(x),若x+y>0,则f(x)+f(y)的符号是否确定？反过来，若f(x)+

f(y)>0,则x+y是否一定大于零？

解:∵x+y>0,∴x>－y.

∴f(x)>f(－y).

又f(x)满足f(－x)=－f(x),

∴f(－y)=－f(y).∴f(x)>－f(y).

即f(x)+f(y)>0,故f(x)+f(y)的符号为正.

反过来，由于f(x)+f(y)>0,则得f(x)>－f(y)=f(－y).

又f(x)在R上递增，∴x>－y,即x+y>0.

练习册系列答案

人教金学典同步解析与测评学考练系列答案

小助手课时一本通系列答案

相关题目

下列论断

①函数y＝2x²＋x＋1在(0，＋∞)上不是增函数

②函数y＝在(－∞，－1)∪(－1，＋∞)上是减函数

③函数y＝的单调减区间为[－2，＋∞)

④已知f(x)是R上增函数，若a＋b＞0，则f(a)＋f(b)＞f(－a)＋f(－b)其中正确的序号为________．

已知f(x)是R上的单调函数，且对任意的实数a∈R，有f(a)＋f(－a)＝O恒成立，若f(－3)＝2．

(1)试判断f(X)在R上的单调性，并说明理由；

(2)解关于x的不等式：f()＋f(m)＜0，其中m∈R且m＞0．

（08年新建二中模拟文） (12分) 已知是定义在R上的函数，其图象交x轴于A、B、C三点．若点B的坐标为 (2，0)，且f (x) 在[－1，0]和[4，5]上有相同的单调性，在[0，2]和[4，5]上有相反的单调性．
　　(1)求c的值；
　　(2)在函数f (x)的图象上是否存在一点M(x₀，y₀)，使得f (x)在点M的切线斜率为3b？若存在，求出点M的坐标；若不存在，请说明理由；
　　(3)求| AC |的取值范围．

已知定义在实数集上的函数y=f(x)满足条件:对于任意的x、y∈R, f(x+y)=f(x)+f(y).

(1)求证:f(0)=0;

(2)求证:f(x)是奇函数,试举出两个这样的函数;

(3)若当x＞0时,f(x)＜0.

①试判断函数f(x)在R上的单调性,并证明之;

②判断函数|f(x)|=a所有可能的解的个数,并求出对应的a的范围.

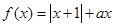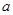已知函数(∈R). 若函数f(x)在 R 上具有单调性，则的取值范围为_________________.

试题分类