题目内容
已知 是奇函数,当
是奇函数,当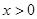 时,
时, 则
则 时,
时, ( )
( )
| A.1 | B.3 | C.-3 | D.-1 |
C
解析试题分析:根据题意,因为函数 是奇函数,则可知f(-x)=-f(x),则f(-1)=-f(1)=-(1+2)=-3,故选C.
是奇函数,则可知f(-x)=-f(x),则f(-1)=-f(1)=-(1+2)=-3,故选C.
考点:函数奇偶性
点评:利用奇偶性的对称性,可以根据x的函数值得到-x的函数值,这是重要的运用。属于基础题。

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
已知函数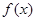 是定义在
是定义在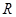 上的单调增函数且为奇函数,数列
上的单调增函数且为奇函数,数列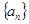 是等差数列,
是等差数列,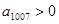 ,则
,则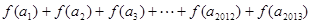 的值( ).
的值( ).
| A.恒为正数 | B.恒为负数 | C.恒为0 | D.可正可负 |
下列函数中,在区间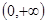 为增函数的是( )
为增函数的是( )
A.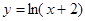 | B.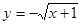 | C. | D.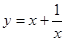 |
若函数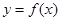
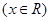 的图象关于直线
的图象关于直线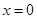 及直线
及直线 对称,且
对称,且 时,
时,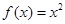 ,则
,则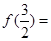 ( )
( )
A.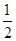 | B.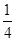 | C. | D.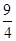 |
函数 的零点所在的区间是( )
的零点所在的区间是( )
A. | B. | C. | D. |
函数 的定义域为
的定义域为
A.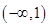 | B.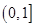 | C.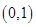 | D.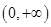 |
下列函数中,值域是 的函数为
的函数为
A. | B. |
C. | D. |
对于定义域为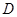 的函数
的函数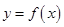 和常数
和常数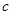 ,若对任意正实数
,若对任意正实数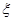 ,
,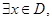 使得
使得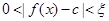 恒成立,则称函数
恒成立,则称函数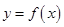 为“敛
为“敛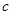 函数”.现给出如下函数:
函数”.现给出如下函数:
①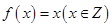 ; ②
; ②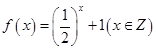 ;
;
③ 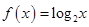 ; ④
; ④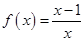 .
.
其中为“敛1函数”的有
| A.①② | B.③④ | C.②③④ | D.①②③ |