题目内容
13.已知2x≤16且${log_2}x≥\frac{1}{2}$,求函数$f(x)={log_2}\frac{x}{2}•{log_{\sqrt{2}}}\frac{{\sqrt{x}}}{2}$的值域.分析 先求出$\frac{1}{2}$≤log2x≤2,再根据二次函数即可得到结论.
解答 解:由2x≤16得x≤4,log2x≤2,
即$\frac{1}{2}$≤log2x≤2,
$f(x)={log_2}\frac{x}{2}•{log_{\sqrt{2}}}\frac{{\sqrt{x}}}{2}$=(log2x-1)(log2x-2)=(log2x-$\frac{3}{2}$)2-$\frac{1}{4}$,
当${log_2}x=\frac{3}{2}$,$f{(x)_{min}}=-\frac{1}{4}$,当${log_2}x=\frac{1}{2}$,$f{(x)_{max}}=\frac{3}{4}$,
故f(x)的取值范围为$[-\frac{1}{4},\frac{3}{4}]$.
点评 本题主要考查函数值域的计算,根据二次函数是解决本题的关键.

练习册系列答案
相关题目
4.在区间[0,9]上随机取一实数x,则该实数x满足不等式1≤log2x≤2的概率为( )
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{7}{9}$ |
18.设$f(x)=\left\{\begin{array}{l}{2^x},x∈[{0,2}]\\ x+1,x∈[{-2,0})\end{array}\right.$,在集合M={y|y=f(x)}中随机取一个数m,则事件“m>0”的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{1}{5}$ |
6.已知方程$\frac{{x}^{2}}{{m}^{2}+n}$-$\frac{{y}^{2}}{3{m}^{2}-n}$=1表示双曲线,且该双曲线两焦点间的距离为4,则n的取值范围是(-1,3).
7.设全集U={1,2,3,4,5},集合A={1,3},B={3,5},则∁U(A∪B)=( )
| A. | {1,4} | B. | {1,5} | C. | {2,4} | D. | {2,5} |
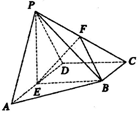 在四棱锥P-ABCD中,E为棱AD的中点,PE⊥平面ABCD,AD∥BC,∠ADC=90°,ED=BC=2,EB=3,F为棱PC的中点.
在四棱锥P-ABCD中,E为棱AD的中点,PE⊥平面ABCD,AD∥BC,∠ADC=90°,ED=BC=2,EB=3,F为棱PC的中点.