题目内容
过点A（-1，1），B（1，-1），且圆心在直线x+y-2=0上的圆的方程是( )A.（x-3）2+(y+1)2=4 B.（x+3）2+(y-1)2=4
C.（x-1）2+(y-1)2=4 D.（x+1）2+(y+1)2=4
思路解析：选择题可以有许多灵活的解法,如排除法，特例法等.另外，也可以考虑待定系数法求解. 解法一：（排除法）由于点A在圆上，故A的坐标（-1，1）是圆的方程的一组解，验证排除A；同理得点B在圆上，排除B；圆心在x+y-2=0上，排除D.故选C. 解法二：设圆心（a,2-a），半径为r，则圆心方程为(x-a)2+(y-2+a)2=r2. 由题意得 ∴圆的方程是（x-1）2+(y-1)2=4. 故选C. 解法三：由题意知AB的中垂线与直线x+y-2=0的交点就是圆心. AB的中垂线：y+0=1×(x-0)，即x-y=0. ∴ 解得x=1,y=1, 即圆心为（1,1）. 则半径r= ∴圆的方程为(x-1)2+(y-1)2=4. 故选C.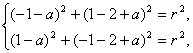
解得a=1,r2=4.
=2.
名校调研跟踪测试卷系列答案
好成绩1加1学习导航系列答案
金牌训练系列答案
数海探究系列答案
快乐练练吧北京交通大学出版社系列答案
双基同步AB卷系列答案
同步训练作业本系列答案
品学双优系列答案
已知中心在原点、焦点在x轴上椭圆，离心率为