题目内容
如图,某人在塔的正东方向上的C处在与塔垂直的水平面内沿南偏西60°的方向以每分钟100米的速度步行了 1分钟以后,在点D处望见塔的底端B在东北方向上,已知沿途塔的仰角∠AEB=α,α的最大值为60°.
(1)求该人沿南偏西60°的方向走到仰角α最大时,走了几分钟;
(2)求塔的高AB。
(1)求该人沿南偏西60°的方向走到仰角α最大时,走了几分钟;
(2)求塔的高AB。
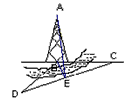
解:(1)依题意知在△DBC中,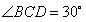 ,
,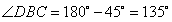 ,
,
CD=100(m),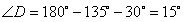 ,
,
由正弦定理得,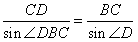 ,
,
∴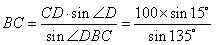
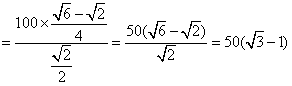 (m),
(m),
在Rt△ABE中,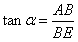 ,
,
∵AB为定长,
∴当BE的长最小时,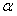 取最大值60°,这时
取最大值60°,这时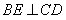 ,
,
当BE⊥CD时,在Rt△BEC中,
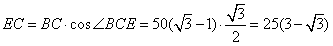 (m),
(m),
设该人沿南偏西60°的方向走到仰角α最大时,走了t分钟,
则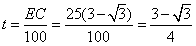 (分钟)。
(分钟)。
(2)由(1)知当α取得最大值60°时,BE⊥CD,
在Rt△BEC中,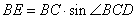 ,
,
∴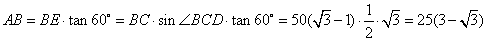 ,
,
即塔高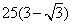 m。
m。
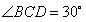 ,
,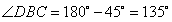 ,
,CD=100(m),
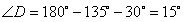 ,
,由正弦定理得,
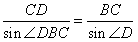 ,
,∴
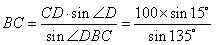
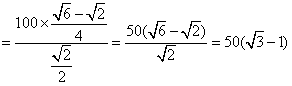 (m),
(m),在Rt△ABE中,
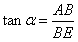 ,
, ∵AB为定长,
∴当BE的长最小时,
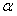 取最大值60°,这时
取最大值60°,这时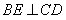 ,
,当BE⊥CD时,在Rt△BEC中,
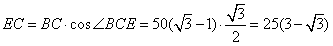 (m),
(m),设该人沿南偏西60°的方向走到仰角α最大时,走了t分钟,
则
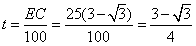 (分钟)。
(分钟)。(2)由(1)知当α取得最大值60°时,BE⊥CD,
在Rt△BEC中,
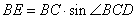 ,
,∴
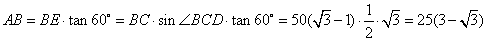 ,
,即塔高
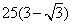 m。
m。
练习册系列答案
相关题目
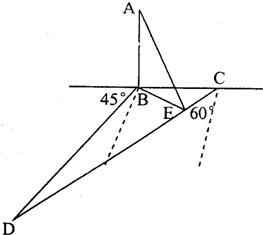 如图,某人在塔AB(塔垂直于地面)的正东C点沿着南偏西60°的方向前进80米后到达D点,望见塔在东北方向,若沿途测得塔的最大仰角为30°(观测点为E),求塔高
如图,某人在塔AB(塔垂直于地面)的正东C点沿着南偏西60°的方向前进80米后到达D点,望见塔在东北方向,若沿途测得塔的最大仰角为30°(观测点为E),求塔高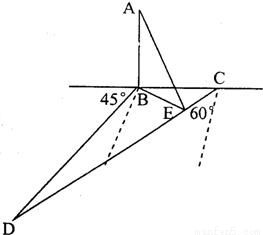 如图,某人在塔AB(塔垂直于地面)的正东C点沿着南偏西60°的方向前进80米后到达D点,望见塔在东北方向,若沿途测得塔的最大仰角为30°(观测点为E),求塔高
如图,某人在塔AB(塔垂直于地面)的正东C点沿着南偏西60°的方向前进80米后到达D点,望见塔在东北方向,若沿途测得塔的最大仰角为30°(观测点为E),求塔高 .
.