题目内容
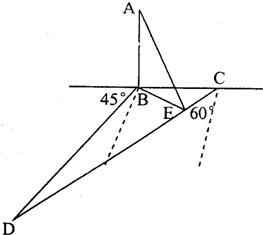 如图,某人在塔AB(塔垂直于地面)的正东C点沿着南偏西60°的方向前进80米后到达D点,望见塔在东北方向,若沿途测得塔的最大仰角为30°(观测点为E),求塔高(sin15°=
如图,某人在塔AB(塔垂直于地面)的正东C点沿着南偏西60°的方向前进80米后到达D点,望见塔在东北方向,若沿途测得塔的最大仰角为30°(观测点为E),求塔高(sin15°=
| ||||
| 4 |
分析:在△BCD中,由正弦定理得
=
可求BD,在Rt△BED中,由题意可求∠BDE,而由BE=DBsin∠BDE可求BE,然后由AB=BEtan∠AEB可求AB即塔高
| CD |
| sin∠DBC |
| BD |
| sin∠BCD |
解答:解:在△BCD中,CD=80,∠BCD=30°,∠DBC=135°
由正弦定理得
=
BD=
=40
…(5分)
由题意BE⊥CD∴在Rt△BED中,∠BDE=180°-135°-30°=15°
∴DE=DBsin15°=40
•
=20
-1…(9分)
在Rt△ABE中,∠AEB=30°∴AB=BEtan30°=20(
-1)•
=
(3-
)…(11分)
故所求塔高为
(3-
)米. …(12分)
由正弦定理得
| CD |
| sin∠DBC |
| BD |
| sin∠BCD |
BD=
| 80sin30° |
| sin135° |
| 2 |
由题意BE⊥CD∴在Rt△BED中,∠BDE=180°-135°-30°=15°
∴DE=DBsin15°=40
| 2 |
| ||||
| 4 |
| 3 |
在Rt△ABE中,∠AEB=30°∴AB=BEtan30°=20(
| 3 |
| ||
| 3 |
| 20 |
| 3 |
| 3 |
故所求塔高为
| 20 |
| 3 |
| 3 |
点评:本题主要考察了实际问题的求解,解题的关键是要把实际问题转化为数学问题,然后结合合适的公式进行求解.

练习册系列答案
相关题目
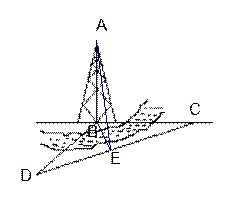
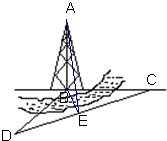 如图,某人在塔的正东方向上的C处在与塔垂直的水平面内沿南偏西60°的方向以每小时6千米的速度步行了1分钟以后,在点D处望见塔的底端B在东北方向上,已知沿途塔的仰角∠AEB=α,α的最大值为60°.
如图,某人在塔的正东方向上的C处在与塔垂直的水平面内沿南偏西60°的方向以每小时6千米的速度步行了1分钟以后,在点D处望见塔的底端B在东北方向上,已知沿途塔的仰角∠AEB=α,α的最大值为60°.
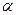 ,
, .
.

 ,
, .
.
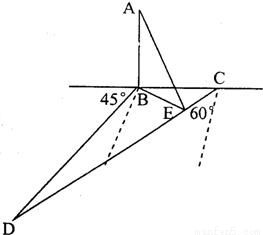 如图,某人在塔AB(塔垂直于地面)的正东C点沿着南偏西60°的方向前进80米后到达D点,望见塔在东北方向,若沿途测得塔的最大仰角为30°(观测点为E),求塔高
如图,某人在塔AB(塔垂直于地面)的正东C点沿着南偏西60°的方向前进80米后到达D点,望见塔在东北方向,若沿途测得塔的最大仰角为30°(观测点为E),求塔高 .
.