题目内容
已知函数 的导函数
的导函数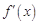 是二次函数,当
是二次函数,当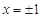 时,
时, 有极值,且极大值为2,
有极值,且极大值为2,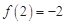 .
.
(1)求函数 的解析式;
的解析式;
(2)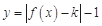 有两个零点,求实数
有两个零点,求实数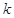 的取值范围;
的取值范围;
(3)设函数 ,若存在实数
,若存在实数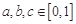 ,使得
,使得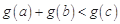 ,求
,求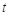 的取值范围.
的取值范围.
(1)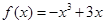 ;(2)
;(2)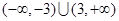 ;(3)
;(3) .
.
解析试题分析:(1)先通过函数 的导函数
的导函数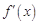 是二次函数,且当
是二次函数,且当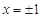 时,
时, 有极值将函数
有极值将函数 的导函数设出来:
的导函数设出来: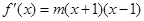 .从而可设
.从而可设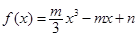 ,其中
,其中 为常数.再由
为常数.再由 极大值为2及
极大值为2及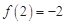 将
将 求出.注意,
求出.注意, 极大值为2,即
极大值为2,即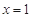 或
或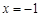 时,函数值为2.结合
时,函数值为2.结合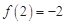 正好可以将其中一种情况舍去,从而解出
正好可以将其中一种情况舍去,从而解出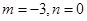 ,于是得到函数
,于是得到函数 的解析式;(2)由
的解析式;(2)由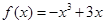 ,
, 列出表格,分析函数
列出表格,分析函数 的单调性和极值.
的单调性和极值.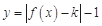 有两个零点,即方程
有两个零点,即方程 有两个根,而
有两个根,而 ,即方程
,即方程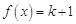 与方程
与方程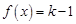 各只有一个解.结合函数
各只有一个解.结合函数 的单调性和极值,发现方程
的单调性和极值,发现方程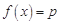 只有当
只有当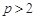 或
或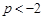 时才只有一个解.所以有
时才只有一个解.所以有 或
或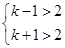 或
或 ,从而解得
,从而解得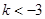 或
或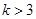 ;(3)由于存在实数
;(3)由于存在实数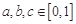 ,使得
,使得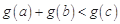 ,也就是说
,也就是说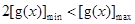 ,否则就不存在实数
,否则就不存在实数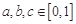 ,使得
,使得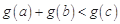 .因此本题转化为求
.因此本题转化为求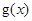 在
在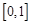 上的最大值与最小值.根据条件可得
上的最大值与最小值.根据条件可得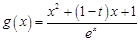 ,所以其导函数
,所以其导函数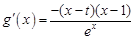 .然后讨论
.然后讨论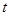 的范围以得到
的范围以得到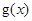 在
在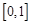 上单调性,从而找出最值.再通过不等式
上单调性,从而找出最值.再通过不等式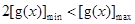 得到
得到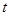 的取值范围.注意当
的取值范围.注意当 时比较麻烦,
时比较麻烦,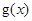 在
在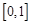 上先减后增,
上先减后增,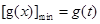 ,而最大值无法确定是
,而最大值无法确定是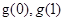 中的哪一个,所以我们用
中的哪一个,所以我们用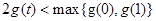 来表示不等式
来表示不等式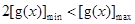 .
.
试题解析:(1)由条件,可设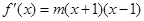 ,则
,则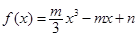 ,其中
,其中 为常数.
为常数.
因为 极大值为2.所以
极大值为2.所以 或
或 ,即
,即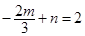 或
或 .由
.由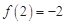 得
得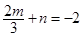 ①.所以
①.所以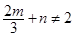 ,即
,即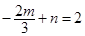 ②.由①②可得,
②.由①②可得,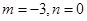 .所以
.所以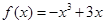 .
.
(2)由(1),得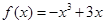 ,即
,即 .列表:
.列表:
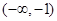

一通百通小学毕业升学模拟测试卷系列答案
真题集训小学期末全程测试卷系列答案
100分闯关考前冲刺全真模拟系列答案
启航学期总动员系列答案
全国历届中考真题分类一卷通系列答案
考卷王单元检测评估卷系列答案

典元教辅小学毕业升学必备小升初押题卷系列答案
金榜夺冠真题卷系列答案
小升初综合素质检测卷系列答案
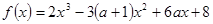 ,其中
,其中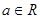 .
.  在
在 处取得极值,求常数
处取得极值,求常数 的值;
的值; ,
, ,若
,若 元素中有唯一的整数,求
元素中有唯一的整数,求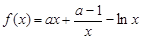
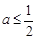 时,试讨论函数
时,试讨论函数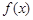 的单调性;
的单调性;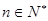 ,有
,有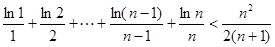 .
.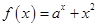 ,
,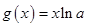 ,
,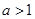 .
.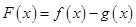 在
在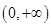 上单调递增;
上单调递增;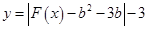 有四个零点,求
有四个零点,求 的取值范围.
的取值范围.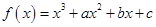 ,曲线
,曲线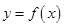 在点
在点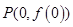 处的切线是
处的切线是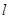 :
: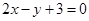
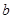 ,
,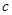 的值;
的值; 在
在 上单调递增,求
上单调递增,求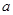 的取值范围
的取值范围 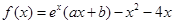 ,曲线
,曲线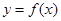 在点
在点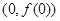 处切线方程为
处切线方程为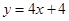 。
。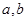 的值;
的值;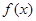 的单调性,并求
的单调性,并求
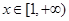 ,使得
,使得 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;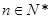 ,不等式
,不等式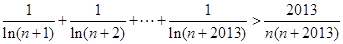 成立.
成立. (
( ).
).  时,求函数
时,求函数 的单调区间;
的单调区间; 时,
时, ,求函数
,求函数 上的最小值;
上的最小值; ,都有
,都有 .
.