题目内容
已知函数 (
( ).
).
(1)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)当 时,
时, 取得极值.
取得极值.
① 若 ,求函数
,求函数 在
在 上的最小值;
上的最小值;
② 求证:对任意 ,都有
,都有 .
.
(1)单调增区间为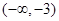 和
和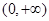 ,单调减区间为
,单调减区间为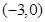 ;(2)①
;(2)①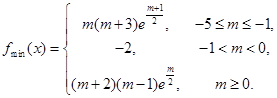 ②详见解析.
②详见解析.
解析试题分析:(1)求导解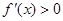 得
得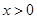 或
或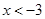 , 解
, 解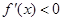 得
得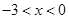 ;
;
(2)①当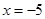 时,
时, 取得极值, 所以
取得极值, 所以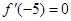 解得
解得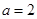 ,对
,对 求导,判断在
求导,判断在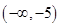 ,
,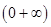 递增,在
递增,在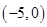 递减,分类讨论,求出最小值;②通过求导,求出
递减,分类讨论,求出最小值;②通过求导,求出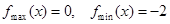 ,将恒成立问题转化为最值问题,对任意
,将恒成立问题转化为最值问题,对任意 ,都有
,都有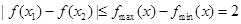 .
.
试题解析:(1)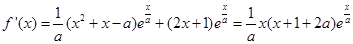
当 时,
时,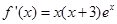
解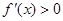 得
得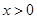 或
或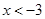 , 解
, 解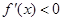 得
得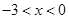
所以 单调增区间为
单调增区间为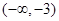 和
和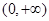 ,单调减区间为
,单调减区间为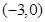
(2)①当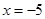 时,
时, 取得极值, 所以
取得极值, 所以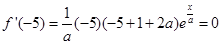
解得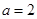 (经检验
(经检验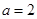 符合题意)
符合题意) 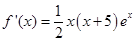
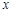
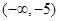
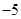
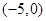

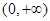
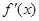
+ 0 - 0 + 
 ↗
↗ 练习册系列答案
练习册系列答案

每时每刻快乐优加系列答案
孟建平培优一号系列答案
孟建平毕业总复习系列答案
密解1对1系列答案
名师导练系列答案
名师讲堂单元同步学练测系列答案
名师面对面中考满分特训方案系列答案
名师名卷单元月考期中期末系列答案
初中总复习教学指南系列答案
相关题目
 的导函数
的导函数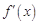 是二次函数,当
是二次函数,当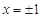 时,
时,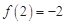 .
.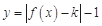 有两个零点,求实数
有两个零点,求实数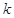 的取值范围;
的取值范围; ,若存在实数
,若存在实数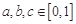 ,使得
,使得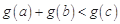 ,求
,求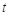 的取值范围.
的取值范围.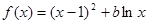 ,其中
,其中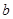 为常数。
为常数。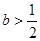 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性;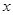 个月内,对某种商品的需求总量
个月内,对某种商品的需求总量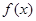 (万件)近似满足:
(万件)近似满足: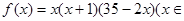 N*,且
N*,且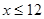 )
)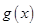 (万件)与月份
(万件)与月份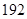 万件;
万件; 万件(不包含积压商品),要保证每月都满足供应,
万件(不包含积压商品),要保证每月都满足供应,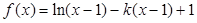 .
.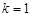 时,求函数
时,求函数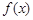 的最大值;
的最大值;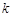 的取值范围;
的取值范围;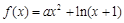 .
.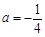 时,求函数
时,求函数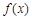 的单调区间;
的单调区间;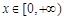 时,不等式
时,不等式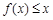 恒成立,求实数
恒成立,求实数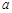 的取值范围.
的取值范围.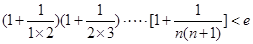 (
(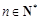 ,e是自然对数的底数).
,e是自然对数的底数).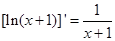
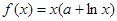 有极小值
有极小值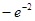 .
.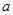 的值;
的值;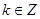 ,且
,且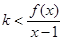 对任意
对任意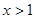 恒成立,求
恒成立,求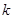 的最大值为.
的最大值为.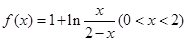 .
.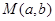 ,使得函数
,使得函数 的图像上任意一点P关于点M对称的点Q也在函数
的图像上任意一点P关于点M对称的点Q也在函数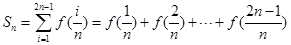 ,其中
,其中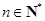 ,求
,求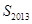 ;
;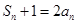 ,若不等式
,若不等式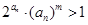 对
对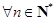 且
且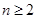 恒成立,求实数
恒成立,求实数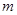 的取值范围.
的取值范围. ,点
,点 为一定点,直线
为一定点,直线 分别与函数
分别与函数 的图象和
的图象和 轴交于点
轴交于点 ,
, ,记
,记 的面积为
的面积为 .
. 时,求函数
时,求函数 时, 若
时, 若 ,使得
,使得 , 求实数
, 求实数 的取值范围.
的取值范围.