题目内容
10.已知直线ax-2by=2(a>0,b>0)过圆x2+y2-4x+2y+1=0的圆心,则$\frac{1}{a}+\frac{1}{b}$的最小值为4.分析 圆心为(2,-1),则代入直线得:2a+2b=2,即a+b=1,利用基本不等式,即可求出$\frac{1}{a}+\frac{1}{b}$的最小值.
解答 解:圆心为(2,-1),则代入直线得:2a+2b=2,即a+b=1,则有$\frac{1}{a}+\frac{1}{b}=\frac{a+b}{a}+\frac{a+b}{b}=2+\frac{b}{a}+\frac{a}{b}≥2+2\sqrt{\frac{b}{a}•\frac{a}{b}}=4$,(当且仅当$a=b=\frac{1}{2}$时取等号)
故答案为4.
点评 本题考查直线与圆的位置关系,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
15.等差数列{an}前n项和为Sn,S7+S5=10,a3=5,则S7=( )
| A. | 25 | B. | 49 | C. | -15 | D. | 40 |
19.在数列{an}中,a1=1,an+1=2an,${S_n}=a_1^2-a_2^2+a_3^2-a_4^2+$…$+a_{2n-1}^2-a_{2n}^2$等于( )
| A. | $\frac{1}{3}({2^n}-1)$ | B. | $\frac{1}{5}(1-{2^{4n}})$ | C. | $\frac{1}{3}({4^n}-1)$ | D. | $\frac{1}{3}(1-{2^n})$ |
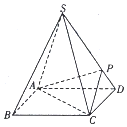 如图,四棱锥S-ABCD的底面边长为1的正方形,每条侧棱的长均为$\sqrt{2}$,P为侧棱SD上的点.
如图,四棱锥S-ABCD的底面边长为1的正方形,每条侧棱的长均为$\sqrt{2}$,P为侧棱SD上的点.