题目内容
古希腊毕达哥拉斯学派的数学家研究过各种多边形数。如三角形数1,3,6,10···,第n个三角形数为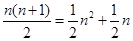 。记第n个k边形数为N(n,k)(
。记第n个k边形数为N(n,k)(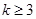 ),以下列出了部分k边形数中第n个数的表达式:
),以下列出了部分k边形数中第n个数的表达式:
三角形数 N(n,3)=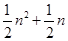
正方形数 N(n,4)=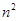
五边形数 N(n,5)=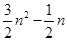
六边形数 N(n,6)=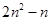
可以推测N(n,k)的表达式,由此计算N(10,24)= ____________

解析试题分析:原已知式子可化为: ,
, ,
, ,
, ,由此归纳推理可得
,由此归纳推理可得 ,
, .
.
故答案为: .
.
考点:归纳推理的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
用反证法证明命题“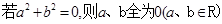 ”,其反设正确的是( )
”,其反设正确的是( )
A.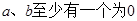 | B.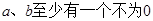 |
C.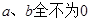 | D. |
观察式子: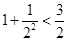 ,
,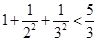 ,
,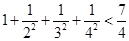 ,……则可归纳出式子(
,……则可归纳出式子(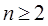 )( )
)( )
A. | B.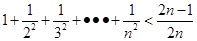 |
C.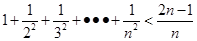 | D.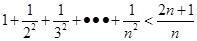 |
下列推理中属于归纳推理且结论正确的是( )
| A.设数列{an}的前n项和为Sn.由an=2n-1,求出S1=12,S2=22,S3=32,…,推断:Sn=n2 |
| B.由f(x)=xcos x满足f(-x)=-f(x)对?x∈R都成立,推断:f(x)=xcos x为奇函数 |
C.由圆x2+y2=r2的面积S=πr2,推断:椭圆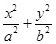 =1(a>b>0)的面积S=πab =1(a>b>0)的面积S=πab |
| D.由(1+1)2>21,(2+1)2>22,(3+1)2>23,…,推断:对一切n∈N*,(n+1)2>2n |
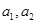 是正实数,则有
是正实数,则有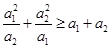 ”推广到一般情形,推广后的命题为____________.
”推广到一般情形,推广后的命题为____________.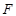 )
)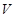 )
)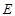 )
)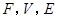 所满足的等式是_________.
所满足的等式是_________.  ,则对于
,则对于 ,
, .
. 的前
的前 项和为
项和为 ,则
,则 ,
, ,
, ,
,
 的前
的前 ,则
,则 成等比数列.
成等比数列.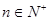 ,
, ,由计算得
,由计算得 ,
, ,
, ,
, ,观察上述结果,可推出一般的结论为 .
,观察上述结果,可推出一般的结论为 .