题目内容
设{an}是公比为q的等比数列，|q|＞1，令bn=an+1（n=1，2，3…），若数列{bn}有连续四项在集合{-53，-23，19，37，82}中，则q2= ．
考点：等比数列的通项公式
专题：等差数列与等比数列
分析：由题设条件可得{an}公比为q的等比数列，它有连续四项在集合{-54，-24，18，36，81}中，即可判断出两个负数-54，-24是数列中的两项，且序号相差2，由此即可得到公比的方程，求解即可得到答案．
解答：
解：由题意知，{an}是公比为q的等比数列，
由数列{bn}有连续四项在集合{-53，-23，19，37，82}中，
可得{an}有连续四项在集合{-54，-24，18，36，81}中，
由于集合中仅有三个正数，两个负数，
故{an}各项中必有两个为负数，所以公比为负即q＜0，
由于两个负数分别为-54，-24，故q2=
或
，
因为|q|＞1，所以q2=
，
故答案为：
．
由数列{bn}有连续四项在集合{-53，-23，19，37，82}中，
可得{an}有连续四项在集合{-54，-24，18，36，81}中，
由于集合中仅有三个正数，两个负数，
故{an}各项中必有两个为负数，所以公比为负即q＜0，
由于两个负数分别为-54，-24，故q2=
| 9 |
| 4 |
| 4 |
| 9 |
因为|q|＞1，所以q2=
| 9 |
| 4 |
故答案为：
| 9 |
| 4 |
点评：本题考查等比数列的性质，解题的关键是判断出两个负数-54，-24是数列中的两项，由等比数列的性质得关于公比的方程，考查判断推理能力及转化的思想．
练习册系列答案
备战中考寒假系列答案
相关题目
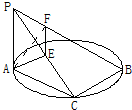如图PA⊥⊙O所在平面，AB是⊙O的直径，C是⊙O上一点，E、F分别是点A在PC、PB上的射影，给出下列结论：