题目内容
已知直角坐标平面内的两个向量
=（1，3），
=（m，2m-3），使得平面内的任意一个向量
都可以唯一的表示成=
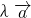+μ，则m的取值范围是 ________．
m∈R且m≠-3
分析：根据平面向量的基本定理知基底向量不共线，由向量共线的坐标表示求出m的范围．
解答：根据平面向量的基本定理知，与不共线，
即2m-3-3m≠0，解得m≠-3，m的取值范围是m∈R且m≠-3．
故答案为：m∈R且m≠-3．
点评：本题考查了平面向量的基本定理内容，利用向量共线的坐标表示进行求解，是对基础知识的考查．
分析：根据平面向量的基本定理知基底向量不共线，由向量共线的坐标表示求出m的范围．
解答：根据平面向量的基本定理知，
与不共线，即2m-3-3m≠0，解得m≠-3，m的取值范围是m∈R且m≠-3．
故答案为：m∈R且m≠-3．
点评：本题考查了平面向量的基本定理内容，利用向量共线的坐标表示进行求解，是对基础知识的考查．
练习册系列答案
名校课堂系列答案
相关题目
已知直角坐标平面内的动点M满足：|MA|2-|MB|2=4（|MB|-1），其中A（0，-1），B（0，1）．
，
，使得平面内任何一个向量
都可以唯一表示成
，则
的取值范围是（
）
B.
C.
D.
[网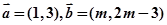
，使得平面内的任意一个向量
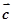都可以唯一的表示成
，则
的取值范围是 .