题目内容
 已知直角坐标平面内的动点M满足:|MA|2-|MB|2=4(|MB|-1),其中A(0,-1),B(0,1).
已知直角坐标平面内的动点M满足:|MA|2-|MB|2=4(|MB|-1),其中A(0,-1),B(0,1).(Ⅰ)求动点M的轨迹C的方程;
(Ⅱ)过N(-2,1)作两条直线交(Ⅰ)中轨迹C于P,Q,并且都与“以A为圆心,r为半径的动圆”相切,求证:直线PQ经过定点.
分析:(1)设M(x,y),由|MA|2-|MB|2=4(|MB|-1)可得方程,化简即可;
(2)设NQ、NP直线斜率分别为k1,k2,利用点斜式可写出直线NQ、NP的方程,根据NQ、NP与动圆A相切可得k1k2=1,分别联立直线与曲线方程可得Q、P坐标,由点斜式可写出直线PQ的方程,据方程形式即可求得所过定点.
(2)设NQ、NP直线斜率分别为k1,k2,利用点斜式可写出直线NQ、NP的方程,根据NQ、NP与动圆A相切可得k1k2=1,分别联立直线与曲线方程可得Q、P坐标,由点斜式可写出直线PQ的方程,据方程形式即可求得所过定点.
解答:解:(1)设M(x,y),由|MA|2-|MB|2=4(|MB|-1),
得x2+(y+1)2-[x2+(y-1)2]=4(
-1),
化简得:x2=4y.
(2)设NQ、NP直线斜率分别为k1,k2,则直线NQ:y-1=k1(x+2),即:k1x-y+2k1+1=0,
NP:y-1=k2(x+2),即:k2x-y+2k2+1=0,
由NQ、NP与动圆A相切得:
=
,
化简得:(k1-k2)(k1k2-1)=0,
∵k1≠k2,∴k1k2=1,
联立
,解得Q(4k1+2,(2k1+1)2),
同理:P(4k2+2,(2k2+1)2),
∴kPQ=
=k1+k2+1,
∴PQ:y-(2k2+1)2=(k1+k2+1)[x-(4k2+2)],
化简得:y=(k1+k2+1)(x-2)-3,
所以直线PQ恒过定点(2,-3).
得x2+(y+1)2-[x2+(y-1)2]=4(
| x2+(y-1)2 |
化简得:x2=4y.
(2)设NQ、NP直线斜率分别为k1,k2,则直线NQ:y-1=k1(x+2),即:k1x-y+2k1+1=0,
NP:y-1=k2(x+2),即:k2x-y+2k2+1=0,
由NQ、NP与动圆A相切得:
| 2|k1+1| | ||
|
| 2|k2+1| | ||
|
化简得:(k1-k2)(k1k2-1)=0,
∵k1≠k2,∴k1k2=1,
联立
|
同理:P(4k2+2,(2k2+1)2),
∴kPQ=
| (2k2+1)2-(2k1+1)2 |
| 4(k2-k1) |
∴PQ:y-(2k2+1)2=(k1+k2+1)[x-(4k2+2)],
化简得:y=(k1+k2+1)(x-2)-3,
所以直线PQ恒过定点(2,-3).
点评:本题考查直线与圆锥曲线的综合问题、圆锥曲线的轨迹问题,考查学生的运算能力,考查学生综合运用知识分析问题解决问题的能力,综合性较强,有一定难度.

练习册系列答案
相关题目
 ,
, ,使得平面内任何一个向量
,使得平面内任何一个向量 都可以唯一表示成
都可以唯一表示成 ,则
,则 的取值范围是(
)
的取值范围是(
) B.
B. C.
C. D.
D. [网
[网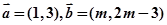 ,使得平面内的任意一个向量
,使得平面内的任意一个向量 都可以唯一的表示成
都可以唯一的表示成 ,则
,则 的取值范围是 .
的取值范围是 .