题目内容
20.已知f(x)=alnx+$\frac{1}{2}{x^2}$(a>0),若对任意两个不等的正实数x1,x2都有$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}$≥2恒成立,则a的取值范围是( )| A. | (1,+∞) | B. | [1,+∞) | C. | (0,1] | D. | (0,1) |
分析 依题意知,f′(x)=$\frac{a}{x}$+x≥2(x>0)恒成立?a≥2x-x2恒成立,令g(x)=2x-x2=-(x-1)2+1,利用二次函数的对称性、单调性与最值,可求得g(x)max,于是可得a的取值范围.
解答 解:∵f(x)=alnx+$\frac{1}{2}$x2(a>0),对任意两个不等的正实数x1、x2都有>2恒成立,
∴f′(x)=$\frac{a}{x}$+x≥2(x>0)恒成立,
∴a≥2x-x2恒成立,令g(x)=2x-x2=-(x-1)2+1,
则a≥g(x)max,
∵g(x)=2x-x2为开口方向向下,对称轴为x=1的抛物线,
∴当x=1时,g(x)=2x-x2取得最大值g(1)=1,
∴a≥1.
即a的取值范围是[1,+∞).
故选:B.
点评 本题考查函数恒成立问题,考查导数的几何意义与二次函数的对称性、单调性与最值,考查转化思想.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案
相关题目
8.已知函数f(x)=x2+mx+n,且y=f(x+2)的图象关于y轴对称,则大小关系正确的是( )
| A. | f($\frac{5}{2}$)<f(1)<f($\frac{7}{2}$) | B. | f(1)<f($\frac{7}{2}$)<f($\frac{5}{2}$) | C. | f($\frac{7}{2}$)<f(1)<f($\frac{5}{2}$) | D. | f($\frac{7}{2}$)<f($\frac{5}{2}$)<f(1) |
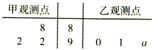 如图,茎叶图记录了某城市甲、乙两个观测点连续三天观测到的空气质量指数(AQI).乙观测点记录中有一个数字模糊无法确认,已知该数是0,1,…,9中随机的一个数,并在图中以a表示.
如图,茎叶图记录了某城市甲、乙两个观测点连续三天观测到的空气质量指数(AQI).乙观测点记录中有一个数字模糊无法确认,已知该数是0,1,…,9中随机的一个数,并在图中以a表示.