题目内容
已知函数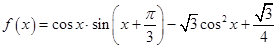 ,
,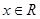 .
.
(1)求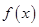 的最小正周期;
的最小正周期;
(2)求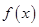 在闭区间
在闭区间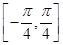 上的最大值和最小值.
上的最大值和最小值.
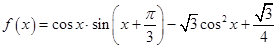 ,
,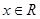 .
.(1)求
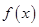 的最小正周期;
的最小正周期;(2)求
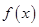 在闭区间
在闭区间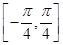 上的最大值和最小值.
上的最大值和最小值.(1) ;(2)最大值为
;(2)最大值为 ,最小值为
,最小值为 .
.
 ;(2)最大值为
;(2)最大值为 ,最小值为
,最小值为 .
.试题分析:
解题思路:利用两角和与差的三角公式和二倍角公式及其变形化成
 的形式,再求周期与最值.
的形式,再求周期与最值.规律总结:涉及三角函数的周期、最值、单调性、对称性等问题,往往先根据三角函数恒等变形化为
 的形式,再利用三角函数的图像与性质进行求解.
的形式,再利用三角函数的图像与性质进行求解.注意点:求
 在给定区间上的最值问题,要注意结合正弦函数或余弦函数的图像求解.
在给定区间上的最值问题,要注意结合正弦函数或余弦函数的图像求解.试题解析:(1)

 ,
,故
 的最小正周期为π.
的最小正周期为π. (2)




函数
 在闭区间
在闭区间 上的最大值为
上的最大值为 ,最小值为
,最小值为 .
. 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
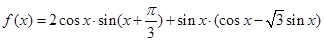
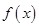 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;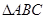 中,
中,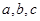 分别是角A、B、C的对边,若
分别是角A、B、C的对边,若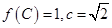 ,求
,求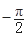 <j<0)图象上的任意两点,且角j的终边经过点P(l,-
<j<0)图象上的任意两点,且角j的终边经过点P(l,-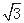 ),若|f(x1)-f(x2)|=4时,|x1-x2|的最小值为
),若|f(x1)-f(x2)|=4时,|x1-x2|的最小值为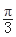 .
. 时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.
时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.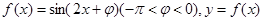 的图象的一条对称轴是直线
的图象的一条对称轴是直线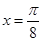 .
.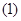 求
求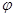 ;
;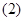 求函数
求函数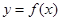 的单调增区间;
的单调增区间;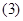 画出函数
画出函数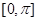 上的图象.
上的图象.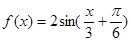 的图象向左平移
的图象向左平移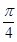 个单位,再向下平移
个单位,再向下平移 个单位,得到函数
个单位,得到函数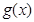 的图象,则
的图象,则



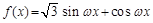 (ω>0)的图象与直线y=-2的两个相邻公共点之间的距离等于π,则
(ω>0)的图象与直线y=-2的两个相邻公共点之间的距离等于π,则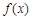 的单调递减区间是( )
的单调递减区间是( )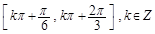
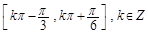
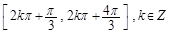
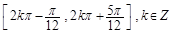
 , 则( ).
, 则( ). 两两为“同形”函数;
两两为“同形”函数; 为“同形”函数,且它们与
为“同形”函数,且它们与 不为“同形”函数;
不为“同形”函数; 为“同形”函数,且它们与
为“同形”函数,且它们与 不为“同形”函数.
不为“同形”函数. 个单位后得到函数
个单位后得到函数 的图象,则
的图象,则 为 .
为 .