题目内容
【题目】已知函数 ![]() ,
, ![]() .
.
(1)当 ![]() 时,求函数
时,求函数 ![]() 的图象在
的图象在 ![]() 处的切线方程;
处的切线方程;
(2)若函数 ![]() 在定义域上为单调增函数.
在定义域上为单调增函数.
①求 ![]() 最大整数值;
最大整数值;
②证明: ![]() .
.
【答案】
(1)解:当 ![]() 时,
时, ![]()
∴ ![]() ,
,
又 ![]() ,∴
,∴ ![]() ,
,
则所求切线方程为 ![]() ,即
,即 ![]()
(2)解:由题意知, ![]() ,
,
若函数 ![]() 在定义域上为单调增函数,则
在定义域上为单调增函数,则 ![]() 恒成立.
恒成立.
①先证明 ![]() .设
.设 ![]() ,则
,则 ![]() ,
,
则函数 ![]() 在
在 ![]() 上单调递减,在
上单调递减,在 ![]() 上单调递增,
上单调递增,
∴ ![]() ,即
,即 ![]() .
.
同理可证 ![]()
∴ ![]() ,∴
,∴ ![]() .
.
当 ![]() 时,
时, ![]() 恒成立.
恒成立.
当 ![]() 时,
时, ![]() ,即
,即 ![]() 不恒成立.
不恒成立.
综上所述, ![]() 的最大整数值为2.
的最大整数值为2.
②由①知, ![]() ,令
,令 ![]() ,
,
∴ ![]()
∴ ![]() .
.
由此可知,当 ![]() 时,
时, ![]() .当
.当 ![]() 时,
时, ![]() ,
,
当 ![]() 时,
时, ![]() ,
, ![]() ,当
,当 ![]() 时,
时, ![]() .
.
累加得 ![]()
![]() .
.
又 ![]()
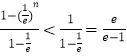 ,
,
∴ ![]()
![]() .
.
【解析】(1)函数的导函数在x=0处的函数值就是函数图象在该点处的切线斜率,用点斜式得到切线方程;
(2)函数在区间上单调递增等价于导函数在区间上恒非负,转化为恒成立问题求a的范围,通过分类讨论得到a的最大整数值;由结论得到一个不等式,令其中t分别取得,2,3...n得到的不等式相加进一步转化为等比数列求和,从而证明不等式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



