Question

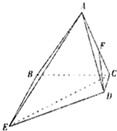（2013•石家庄二模）如图，在四棱锥A-BCDE中，底面BCDE为直角梯形，且BE∥CD，CD⊥BC．侧面ABC⊥底面BCDE，F为AC的中点，BC=BE=4CD=2，AB=AC．
（Ⅰ）求证：FD⊥CE；
（Ⅱ）若规定正视方向与平面ABC 垂直，且四棱锥A-BCDE的侧（左）视图的面积为

3

，求点B到平面ACE的距离．

Answer 1

分析：（Ⅰ）过F作FH⊥BC于H，连接DH，将直角梯形BCDE补成正方形BCGE，连接BG，证明EC⊥平面FHD，即可证得结论；
（Ⅱ）利用V_A-BCE=V_B-ACE，即可求点B到平面ACE的距离．

解答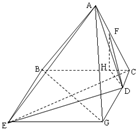：（Ⅰ）证明：过F作FH⊥BC于H，连接DH，将直角梯形BCDE补成正方形BCGE，…（2分）
连接BG
∵侧面ABC⊥底面BCDE，平面ABC∩底面BCDE=BC
∴FH⊥底面BCDE
∴FH⊥BC
∵F为AC的中点，
∴H为BC的四等分点，…（4分）
∵CD=

1

4

CG，∴DH∥BG
∴DH⊥EC
∵FH∩DH=H
∴EC⊥平面FHD
∴FD⊥CE…（6分）
（Ⅱ）解：由题意可知△ABC的高为h=

3

…（8分）
∴AB=AC=2
∴V_A-BCE=

1

3

S△BCE•h=

1

3

•

1

2

•BE•BC•h=

2 3

3

在△AEC中，AE=EC=2

2

，AC=2，S_△AEC=

7

∵V_B-ACE=

1

3

S△AEC•h′
∴h′=

2 21

7

∴点B到平面ACE的距离为

2 21

7

…（12分）

点评：本题考查线面垂直，考查线线垂直，考查点到面距离的计算，正确运用等体积法是解题的关键．