Question

如图，在四棱锥中，底面是菱形，且．

（1）求证：；

（2）若平面与平面的交线为，求证：．

Answer 1

（1）详见解析（2）详见解析

【解析】

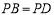试题分析：（1）证明线线垂直，一般利用线面垂直判定与性质定理进行转化证明，先从平面几何条件找垂直：因为四边形ABCD为菱形，所以又因为，O为BD的中点，所以，所以，从而

（2）证明线线平行，一般利用线面平行判定与性质定理进行转化证明，因为四边形ABCD为菱形，所以，因此，从而．

试题解析：

（1）连接AC，交BD于点O，连接PO．

因为四边形ABCD为菱形，所以 2分

又因为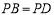，O为BD的中点，

所以 4分

又因为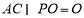

所以，

又因为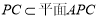

所以 7分

（2）因为四边形ABCD为菱形，所以 9分

因为．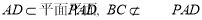

所以 11分

又因为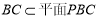，平面平面．

所以． 14分

考点：线面垂直判定与性质定理，线面平行判定与性质定理