题目内容
已知q是等比数列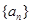 的公比,则“
的公比,则“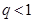 ”是“数列
”是“数列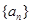 是递减数列”的( )
是递减数列”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
D
解析试题分析:由于对于等比数列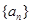 ,当q<1时,如果a<0,则该数列就是递增的数列,因此条件不能推出结论。同时,当数列是递减数列时,则可能q>1,a<0,因此结论不能推出条件,故选D.
,当q<1时,如果a<0,则该数列就是递增的数列,因此条件不能推出结论。同时,当数列是递减数列时,则可能q>1,a<0,因此结论不能推出条件,故选D.
考点:本试题考查了等比数列的单调性的运用。
点评:解决该试题的关键是理解,数列的单调性与其公比之间的关系式的运用。等比数列的单调性,不仅仅取决于公比,还有首项的正负,因此要同时考虑。属于基础题。

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
如果命题“ ”为假命题,则
”为假命题,则
A. 均为假命题 均为假命题 | B. 中至少有一个真命题 中至少有一个真命题 |
C. 均为真命题 均为真命题 | D. 中只有一个真命题 中只有一个真命题 |
“ ”是“直线
”是“直线 与圆
与圆 相交”的
相交”的
| A.充分而不必要条件 |
| B.必要而不充分条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |
①  ;②
;②  ;
;
③ 抛物线
抛物线 过原点;④
过原点;④
其中满足p是q的充要条件的命题个数为
| A.0 | B.1 | C.2 | D.3 |
已知命题 ,
, 则
则 为
为
A. | B. |
C. | D. |
已知 是
是 的内角,则“
的内角,则“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
命题“对任意的 ”的否定是 ( )
”的否定是 ( )
A.不存在 | B.存在 |
C.存在 | D.对任意的 |
下列说法正确的是( )
| A.三点确定一个平面 |
B.平面 和 和 有不同在一条直线上的三个交点 有不同在一条直线上的三个交点 |
| C.梯形一定是平面图形 |
| D.四边形一定是平面图形 |
命题“对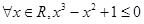 ”的否定是( )
”的否定是( )
| A.不存在x∈R,x3-x2+1≤0 | B.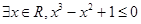 |
C. | D.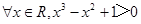 |