Question

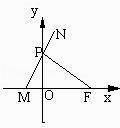
【题目】已知定点F（1，0），动点P（异于原点）在y轴上运动，连接FP，过点P作PM交x轴于点M，并延长MP到点N，且 ， ．
（1）求动点N的轨迹C的方程；
（2）若直线l与动点N的轨迹交于A、B两点，若 且 ，求直线l的斜率k的取值范围．

Answer 1

【答案】
（1）解：设动点N（x，y），则M（﹣x，0），P（0， ）（x＞0），

∵PM⊥PF，∴kPMkPF=﹣1，即 ，

∴y2=4x（x＞0）即为所求

（2）解：设直线l方程为y=kx+b，l与抛物线交于点A（x1，y1）、B（x2，y2），

则由 ，得x1x2+y1y2=﹣4，即 +y1y2=﹣4，∴y1y2=﹣8，

由 可得 ky2﹣4y+4b=0（其中k≠0），∴y1y2= =﹣8，b=﹣2k，

当△=16﹣16kb=16（1+2k2）＞0时，

|AB|2=（1+ ） = [ ﹣4y1y2]= （ +32）．

由题意， ，

可得16×6≤ （ +32）≤16×30，即4≤ ≤28，

即 ，解得 ≤k2≤1，

∴ ≤k≤1，或﹣1≤k≤﹣ ．

即所求k的取值范围是[﹣1，﹣ ]∪[ 1]．

【解析】（1）设出动点N，则M，P的坐标可表示出，利用PM⊥PF，kPMspan>kPF=﹣1，求得x和y的关系式，即N的轨迹方程．（2）设出直线l的方程，A，B的坐标，根据 ，推断出x1x2+y1y2=﹣4进而求得y1y2的值，把直线与抛物线方程联立消去x求得y1y2的表达式，进而气的b和k的关系式，利用弦长公式表示出|AB|2 ， 根据|AB|的范围，求得k的范围．
【考点精析】认真审题，首先需要了解直线的斜率(一条直线的倾斜角α(α≠90°)的正切值叫做这条直线的斜率,斜率常用小写字母k表示,也就是 k = tanα)．