题目内容
已知向量 ,
, .
.(Ⅰ)求
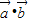 及
及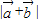 ;
;(Ⅱ)若函数f(x)=
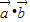 -2t
-2t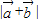 的最小值为
的最小值为 ,求t的值.
,求t的值.
【答案】分析:(Ⅰ)利用向量的数量积公式,结合差角的余弦公式,可求数量积,将模平方,再开方,即可求得模;
(Ⅱ)f(x)=cos2x-4tcosz=2cos2x-4tcosx-1=2(cosx-t)2-2t2-1,再分类讨论,利用函数的最小值,即可确定t的值.
解答:解:(Ⅰ)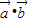 =cos
=cos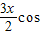
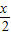 -sin
-sin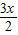 sin
sin =cos2x
=cos2x
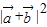 =
= +2
+2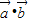 +
+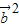 =2+2cos2x=4cos2x,
=2+2cos2x=4cos2x,
∵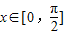 ,∴cosx∈[0,1]
,∴cosx∈[0,1]
∴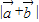 =2cosx
=2cosx
(Ⅱ)f(x)=cos2x-4tcosz=2cos2x-4tcosx-1=2(cosx-t)2-2t2-1
当t<0时,函数在[0,1]上单调增,函数的最小值为-1,不满足;
当0≤t≤1时,函数的最小值为-2t2-1=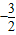 ,∴t=
,∴t= ;
;
当t>1时,函数在[0,1]上单调减,函数的最小值为1-4t=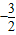 ,t=
,t= ,不满足,
,不满足,
综上可知,t的值为 .
.
点评:本题考查向量的数量积,考查向量的模,考查函数的最值,解题的关键是确定函数的解析式.
(Ⅱ)f(x)=cos2x-4tcosz=2cos2x-4tcosx-1=2(cosx-t)2-2t2-1,再分类讨论,利用函数的最小值,即可确定t的值.
解答:解:(Ⅰ)
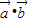 =cos
=cos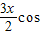
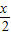 -sin
-sin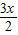 sin
sin =cos2x
=cos2x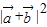 =
= +2
+2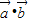 +
+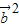 =2+2cos2x=4cos2x,
=2+2cos2x=4cos2x,∵
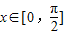 ,∴cosx∈[0,1]
,∴cosx∈[0,1]∴
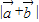 =2cosx
=2cosx(Ⅱ)f(x)=cos2x-4tcosz=2cos2x-4tcosx-1=2(cosx-t)2-2t2-1
当t<0时,函数在[0,1]上单调增,函数的最小值为-1,不满足;
当0≤t≤1时,函数的最小值为-2t2-1=
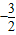 ,∴t=
,∴t= ;
;当t>1时,函数在[0,1]上单调减,函数的最小值为1-4t=
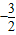 ,t=
,t= ,不满足,
,不满足,综上可知,t的值为
 .
.点评:本题考查向量的数量积,考查向量的模,考查函数的最值,解题的关键是确定函数的解析式.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目











 ,
, 时,求
时,求 的值;
的值; 在
在 上的值域.
上的值域.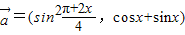 ,
,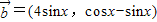 ,
,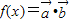
 ,
, ,函数
,函数
 的单调递增区间;
的单调递增区间;
 中,
中, 分别是角
分别是角 的对边,且
的对边,且 ,
, ,
, ,且
,且 ,求
,求 的值.
的值.