题目内容
(本小题满分12分)
已知向量 ,
, ,函数
,函数
(Ⅰ)求 的单调递增区间;
的单调递增区间;
(Ⅱ)在
 中,
中, 分别是角
分别是角 的对边,且
的对边,且 ,
, ,
, ,且
,且 ,求
,求 的值.
的值.
【答案】
(Ⅰ)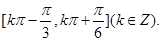 ;(Ⅱ)
;(Ⅱ)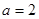 ,
,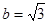 。
。
【解析】
试题分析:(Ⅰ)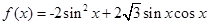
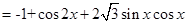
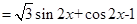
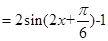 (3分)
(3分)
由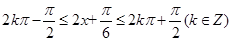 ,
,
得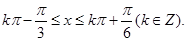 (5分)
(5分)
所以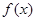 的单调增区间是
的单调增区间是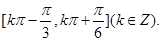 (6分)
(6分)
(2)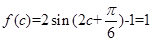
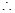
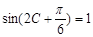
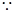
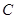 是三角形内角,∴
是三角形内角,∴ 即:
即: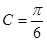 (7分)
(7分)
∴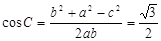 即:
即: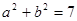 . (9分)
. (9分)
将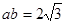 代入可得:
代入可得: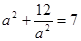 ,解之得:
,解之得: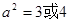
∴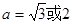 ,
,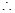
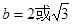 (11分)
(11分)
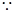
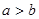 ,∴
,∴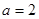 ,
,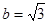 . (12分)
. (12分)
考点:平面向量的数量积;函数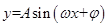 的单调区间;二倍角公式;余弦定理。
的单调区间;二倍角公式;余弦定理。
点评:(1)求三角函数的最值、周期、单调区间时,通常利用公式把三角函数化为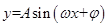 的形式。(2)求函数
的形式。(2)求函数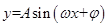 的单调区间时,一定要注意
的单调区间时,一定要注意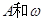 的正负。
的正负。

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目