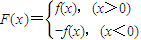题目内容
(1)a,b∈R证明|a+b|≥|a|-|b|,
(2)已知 |x-a|<
,|y-b|<
,求证|(x+y)-(a+b)|<c.
(2)已知 |x-a|<
| c |
| 2 |
| c |
| 2 |
分析:(1)欲证明原不等式成立,考虑到当|a|-|b|≤0时已成立,故只须证明当|a|-|b|>0时成立即可.利用分析法证明即得;
(2)先将原不等式的左边化成|(x-a)+(y-b)|,再利用三角不等式进行放缩即可得到证明.
(2)先将原不等式的左边化成|(x-a)+(y-b)|,再利用三角不等式进行放缩即可得到证明.
解答:证明:(1)当|a|-|b|≤0时,|a+b|≥|a|-|b|成立,
当|a|-|b|>0时,即证明|a+b|2≥(|a|-|b|)2,
整理得 a2+b2+2ab≥a2+b2-2|ab|.
即证ab≥-|ab|
易知上不等式成立,
所以原不等式也成立.
综上,|a+b|≥|a|-|b|,
(2)∵|(x+y)-(a+b)|=|(x-a)+(y-b)|
由三角不等式得,|(x-a)+(y-b)|≤|x-a|+|y-b|<
+
=c.
∴|(x+y)-(a+b)|<c.
当|a|-|b|>0时,即证明|a+b|2≥(|a|-|b|)2,
整理得 a2+b2+2ab≥a2+b2-2|ab|.
即证ab≥-|ab|
易知上不等式成立,
所以原不等式也成立.
综上,|a+b|≥|a|-|b|,
(2)∵|(x+y)-(a+b)|=|(x-a)+(y-b)|
由三角不等式得,|(x-a)+(y-b)|≤|x-a|+|y-b|<
| c |
| 2 |
| c |
| 2 |
∴|(x+y)-(a+b)|<c.
点评:本题主要考查了绝对值不等式的证明,考查了三角不等式的应用,考查了转化思想,属于中档题.

练习册系列答案
相关题目
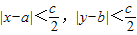 ,求证|(x+y)-(a+b)|<c.
,求证|(x+y)-(a+b)|<c.