题目内容
设函数f(x)=ax2-bx+1(a,b∈R),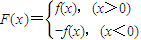
(Ⅰ)若f(1)=0且对任意实数均有f(x)≥0恒成立,求F(x)表达式;
(Ⅱ)在(1)在条件下,当x∈[-3,3]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围;
(Ⅲ)设mn<0,m+n>0,a>0且f(x)为偶函数,证明F(m)>-F(n).
【答案】分析:(Ⅰ)由f(1)=0,可得b=a+1,由f(x)≥0恒成立,即ax2-bx+1≥0恒成立,结合二次函数的性质可得△≤0,可求a,b,进而可求
(Ⅱ)由(Ⅰ)知f(x),g(x),=结合二次函数的单调区间与对称轴的位置关系可求k的范围
(Ⅲ)由f(x)是偶函数,可求b,代入F(x),结合f(x)在[0,+∞)上的单调性可判断F(x)是奇函数,且F(x)在[0,+∞)上为增函数,结合m,n之间的大小关系即可证明
解答:解:(Ⅰ)∵f(1)=0,∴b=a+1,(1分)
由于f(x)≥0恒成立,即ax2-bx+1≥0恒成立,
当a=0时,b=1,此时,f(x)=-x+1与f(x)≥0恒成立矛盾.
当a≠0时,由△=(-b)2-4a=(a+1)2-4a=(a-1)2≤0,得a=1,b=2…(3分)
从而f(x)=x2-2x+1,
∴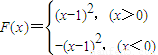 (4分)
(4分)
(Ⅱ)由(Ⅰ)知f(x)=x2-2x+1
∴g(x)=f(x)-kx=x2-(2+k)x+1,其对称为
由g(x)在x∈[-3,3]上是单调函数知: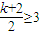 或
或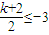 ,
,
解得k≥4或k≤-8(8分)
证明:(Ⅲ)∵f(x)是偶函数,
∴由f(-x)=f(x)得b=0,
故f(x)=ax2+1,
∵a>0,∴f(x)在[0,+∞)上是增函数,(9分)
对于F(x),当x>0时,-x<0,F(-x)=-f(-x)=-f(x)=-F(x)
当x<0时,-x>0,F(-x)=f(-x)=f(x)=-F(x)
∴F(x)是奇函数,且F(x)在[0,+∞)上为增函数.(11分)
∵mn<0,
∴m,n异号,
(1)当m>0,n<0时,由m+n>0得m>-n>0,
∴F(m)>F(-n)=-F(n)
(2)当m<0,n>0时,由m+n>0得n>-m>0,
∴F(n)>F(-m)=-F(m)
即F(m)>-F(n)
综上可知F(m)>-F(n)(14分)
点评:本题综合考查了二次函数的恒成立、二次函数的单调性与对称轴的关系等知识的综合应用,还考查了一定的逻辑推理与运算的能力
(Ⅱ)由(Ⅰ)知f(x),g(x),=结合二次函数的单调区间与对称轴的位置关系可求k的范围
(Ⅲ)由f(x)是偶函数,可求b,代入F(x),结合f(x)在[0,+∞)上的单调性可判断F(x)是奇函数,且F(x)在[0,+∞)上为增函数,结合m,n之间的大小关系即可证明
解答:解:(Ⅰ)∵f(1)=0,∴b=a+1,(1分)
由于f(x)≥0恒成立,即ax2-bx+1≥0恒成立,
当a=0时,b=1,此时,f(x)=-x+1与f(x)≥0恒成立矛盾.
当a≠0时,由△=(-b)2-4a=(a+1)2-4a=(a-1)2≤0,得a=1,b=2…(3分)
从而f(x)=x2-2x+1,
∴
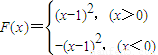 (4分)
(4分)(Ⅱ)由(Ⅰ)知f(x)=x2-2x+1
∴g(x)=f(x)-kx=x2-(2+k)x+1,其对称为

由g(x)在x∈[-3,3]上是单调函数知:
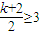 或
或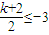 ,
,解得k≥4或k≤-8(8分)
证明:(Ⅲ)∵f(x)是偶函数,
∴由f(-x)=f(x)得b=0,
故f(x)=ax2+1,

∵a>0,∴f(x)在[0,+∞)上是增函数,(9分)
对于F(x),当x>0时,-x<0,F(-x)=-f(-x)=-f(x)=-F(x)
当x<0时,-x>0,F(-x)=f(-x)=f(x)=-F(x)
∴F(x)是奇函数,且F(x)在[0,+∞)上为增函数.(11分)
∵mn<0,
∴m,n异号,
(1)当m>0,n<0时,由m+n>0得m>-n>0,
∴F(m)>F(-n)=-F(n)
(2)当m<0,n>0时,由m+n>0得n>-m>0,
∴F(n)>F(-m)=-F(m)
即F(m)>-F(n)
综上可知F(m)>-F(n)(14分)
点评:本题综合考查了二次函数的恒成立、二次函数的单调性与对称轴的关系等知识的综合应用,还考查了一定的逻辑推理与运算的能力

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 设函数f(x)=(a
设函数f(x)=(a| x |
| 1 | ||
|
| ∫ | 2π π |
A、-
| ||
| B、-160 | ||
| C、160 | ||
| D、20 |