题目内容
已知函数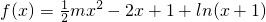
(1)当 时,求函数f(x)的极值点;
时,求函数f(x)的极值点;
(2)当m≤1时,曲线C:y=f(x)在点P(0,1)处的切线l与C有且只有一个公共点,求实数m的范围.
解:(1)当 时,
时,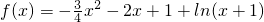 (x>-1)
(x>-1)
∴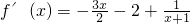 =-
=-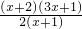
∴x∈(-1,- )时,f′(x)>0;x∈(-
)时,f′(x)>0;x∈(- ,+∞)时,f′(x)<0,
,+∞)时,f′(x)<0,
∴函数f(x)的极值点是x=- ;
;
(2)f′(x)=mx-2+ ,∴f′(0)=-1,∴切线L:y=-x+1
,∴f′(0)=-1,∴切线L:y=-x+1
∵切线L与C有且只有一个公共点,∴ mx2-x+ln(x+1)=0有且只有一个实数解,显然x=0时成立.
mx2-x+ln(x+1)=0有且只有一个实数解,显然x=0时成立.
令g(x)= mx2-x+ln(x+1),则g′(x)=
mx2-x+ln(x+1),则g′(x)=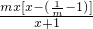
①当m=1时,g′(x)≥0,函数在(-1,+∞)上单调增,x=0是方程唯一实数解;
②当m<1时,由g′(x)=0得x1=0,x2= -1∈(-∞,-1)∪(0,+∞),从而有x=x2是极值点,因此g(x)=0还有一个不是0的解,矛盾
-1∈(-∞,-1)∪(0,+∞),从而有x=x2是极值点,因此g(x)=0还有一个不是0的解,矛盾
综上知,m=1.
分析:(1)求导数,确定函数的单调性,即可求得函数f(x)的极值点;
(2)先求切线方程为y=-x+1,再由切线L与C有且只有一个公共点,转化为 mx2-x+ln(x+1)=0有且只有一个实数解,从而可求实数m的范围.
mx2-x+ln(x+1)=0有且只有一个实数解,从而可求实数m的范围.
点评:本题主要考查导数的运用,考查函数的极值,考查学生分析解决问题的能力,属于中档题.
 时,
时,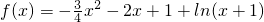 (x>-1)
(x>-1)∴
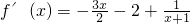 =-
=-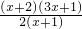
∴x∈(-1,-
 )时,f′(x)>0;x∈(-
)时,f′(x)>0;x∈(- ,+∞)时,f′(x)<0,
,+∞)时,f′(x)<0,∴函数f(x)的极值点是x=-
 ;
;(2)f′(x)=mx-2+
 ,∴f′(0)=-1,∴切线L:y=-x+1
,∴f′(0)=-1,∴切线L:y=-x+1∵切线L与C有且只有一个公共点,∴
 mx2-x+ln(x+1)=0有且只有一个实数解,显然x=0时成立.
mx2-x+ln(x+1)=0有且只有一个实数解,显然x=0时成立.令g(x)=
 mx2-x+ln(x+1),则g′(x)=
mx2-x+ln(x+1),则g′(x)=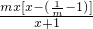
①当m=1时,g′(x)≥0,函数在(-1,+∞)上单调增,x=0是方程唯一实数解;
②当m<1时,由g′(x)=0得x1=0,x2=
 -1∈(-∞,-1)∪(0,+∞),从而有x=x2是极值点,因此g(x)=0还有一个不是0的解,矛盾
-1∈(-∞,-1)∪(0,+∞),从而有x=x2是极值点,因此g(x)=0还有一个不是0的解,矛盾综上知,m=1.
分析:(1)求导数,确定函数的单调性,即可求得函数f(x)的极值点;
(2)先求切线方程为y=-x+1,再由切线L与C有且只有一个公共点,转化为
 mx2-x+ln(x+1)=0有且只有一个实数解,从而可求实数m的范围.
mx2-x+ln(x+1)=0有且只有一个实数解,从而可求实数m的范围.点评:本题主要考查导数的运用,考查函数的极值,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
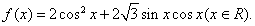
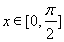
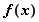

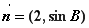
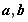

 时,求函数的最大值和最小值;
时,求函数的最大值和最小值; 的取值范围,使
的取值范围,使 在区间
在区间 上是单调减函数
上是单调减函数 .(
.( ).
). 时,求函数
时,求函数 的极值;
的极值; (2)若对
(2)若对 ,有成立,求实数
,有成立,求实数 的取值范围.
的取值范围.
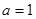 时,求
时,求 的极小值;
的极小值; ,求
,求 的最大值
的最大值 .
.