题目内容
19.某小型餐馆一天装要购买A,B两种蔬菜,A,B蔬菜每千克的单价分别为2元和3元,根据需要,A蔬菜至少要买6千克,B蔬菜至少要买4千克,而且一天中购买这两种蔬菜的总费用不能超过60元,如果这两种蔬菜加工后全部卖出,A,B两种蔬菜交工后每千克分别为2元和1元,则该餐馆的最大利润最大为52元.分析 利用线性规划的内容作出不等式组对应的平面区域,利用线性规划的内容进行图象平移,然后确定目标函数是最值.
解答 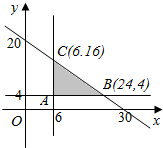 解:依题意,A蔬菜购买的公斤数x和B蔬菜购买的公斤数y之间的满足的不等式组如下:$\left\{\begin{array}{l}2x+3y≤60\\ x≥6\\ y≥4\end{array}\right.$…(3分)
解:依题意,A蔬菜购买的公斤数x和B蔬菜购买的公斤数y之间的满足的不等式组如下:$\left\{\begin{array}{l}2x+3y≤60\\ x≥6\\ y≥4\end{array}\right.$…(3分)
画出的平面区域如图.…(6分)
设餐馆加工这两种蔬菜利润为z元,则目标函数为z=2x+y…(7分)
∵y=-2x+z∴z表示过可行域内点斜率为-2的一组平行线在y轴上的截距.
联立$\left\{\begin{array}{l}2x+3y=60\\ y=4\end{array}\right.$解得$\left\{\begin{array}{l}x=24\\ y=4\end{array}\right.$即B(24,4)…(9分)
∴当直线过点B(24,4)时,在y轴上的截距最大,
即zmax=2×24+4=52…(11分)
答:餐馆应购买A蔬菜24公斤,B蔬菜4公斤,加工后利润最大为52元.…(12分),
故答案为:52
点评 本题主要考查二元一次不等式组表示平面区域的知识,以及线性规划的基本应用,利用数形结合是解决此类问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.曲线f(x)=$\frac{x}{{x}^{2}+1}$在点(1,f(1))处的切线方程是( )
| A. | x=1 | B. | y=$\frac{1}{2}$ | C. | x+y=1 | D. | x-y=1 |
14. 如图,为测得对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东方向是15°方向走30m到位置D,测得∠BDC=30°,则塔高是( )
如图,为测得对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东方向是15°方向走30m到位置D,测得∠BDC=30°,则塔高是( )
 如图,为测得对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东方向是15°方向走30m到位置D,测得∠BDC=30°,则塔高是( )
如图,为测得对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东方向是15°方向走30m到位置D,测得∠BDC=30°,则塔高是( )| A. | 15m | B. | 5$\sqrt{6}$m | C. | 10$\sqrt{6}$m | D. | 15$\sqrt{6}$m |
4.若a=3a+1,b=ln2,c=log2sin$\frac{π}{12}$,则( )
| A. | b>a>c | B. | a>b>c | C. | c>a>b | D. | b>c>a |
9.与两个相交平面的距离都相等的点必在( )
| A. | 一条直线上 | B. | 一个平面上 | C. | 两条直线上 | D. | 两个平面上 |