题目内容
已知Sn为数列{an}的前n项和,且对任意n∈N*,点(an,Sn)都在函数f(x)=-
x+
的图象上.
(1)求{an}的通项公式;
(2)若bn=log
a2n+1,Tn为数列{bn}的前项和,且
+
+…+
≤x2+ax+1对任意正整数n和任意x∈R恒成立,求实数a的取值范围.
| 1 |
| 2 |
| 1 |
| 2 |
(1)求{an}的通项公式;
(2)若bn=log
| 1 |
| 3 |
| 1 |
| T1 |
| 1 |
| T2 |
| 1 |
| Tn |
考点:数列的求和,数列与不等式的综合
专题:等差数列与等比数列
分析:(1)由点(an,Sn)都在函数f(x)=-
x+
的图象上,可得Sn=-
an+
,利用递推式可得an=
an-1,再利用等比数列的通项公式即可得出.
(2)bn=log
a2n+1=log
(
)2n+1=2n+1.利用等差数列的前n项和公式可得Tn=n(n+2),
=
=
(
-
).利用“裂项求和”可得
+
+…+
=
(1+
-
-
)<
,
+
+…+
≤x2+ax+1对任意正整数n和任意x∈R恒成立?
≤x2+ax+1对任意x∈R恒成立?4x2+4ax+1≥0对任意x∈R恒成立?△≤0,解出即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
(2)bn=log
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| Tn |
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
| 1 |
| T1 |
| 1 |
| T2 |
| 1 |
| Tn |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 3 |
| 4 |
| 1 |
| T1 |
| 1 |
| T2 |
| 1 |
| Tn |
| 3 |
| 4 |
解答:
解:(1)∵点(an,Sn)都在函数f(x)=-
x+
的图象上,
∴Sn=-
an+
,
当n=1时,a1=S1=-
a1+
,解得a1=
.
当n≥2时,Sn-1=-
an-1+
,
∴an=Sn-Sn=-
an+
an-1,化为an=
an-1,
∴数列{an}是等比数列,首项为
,公比为
,
∴an=(
)n.
(2)bn=log
a2n+1=log
(
)2n+1=2n+1.
∴Tn=
=n(n+2),
∴
=
=
(
-
).
∴
+
+…+
=
[(1-
)+(
-
)+(
-
)+…+(
-
)+(
-
)]
=
(1+
-
-
)<
(1+
)=
,
+
+…+
≤x2+ax+1对任意正整数n和任意x∈R恒成立?
≤x2+ax+1对任意x∈R恒成立,
?4x2+4ax+1≥0对任意x∈R恒成立,
∴△=16a2-16≤0,解得-1≤a≤1.
∴实数a的取值范围是[-1,1].
| 1 |
| 2 |
| 1 |
| 2 |
∴Sn=-
| 1 |
| 2 |
| 1 |
| 2 |
当n=1时,a1=S1=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
当n≥2时,Sn-1=-
| 1 |
| 2 |
| 1 |
| 2 |
∴an=Sn-Sn=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
∴数列{an}是等比数列,首项为
| 1 |
| 3 |
| 1 |
| 3 |
∴an=(
| 1 |
| 3 |
(2)bn=log
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴Tn=
| n(3+2n+1) |
| 2 |
∴
| 1 |
| Tn |
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
∴
| 1 |
| T1 |
| 1 |
| T2 |
| 1 |
| Tn |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| n-1 |
| 1 |
| n+1 |
| 1 |
| n |
| 1 |
| n+2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| T1 |
| 1 |
| T2 |
| 1 |
| Tn |
| 3 |
| 4 |
?4x2+4ax+1≥0对任意x∈R恒成立,
∴△=16a2-16≤0,解得-1≤a≤1.
∴实数a的取值范围是[-1,1].
点评:本题考查了等比数列的通项公式、“裂项求和”方法、递推式的应用、对数的运算性质、一元二次不等式的解集与判别式的关系,考查了恒成立问题的等价转化方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
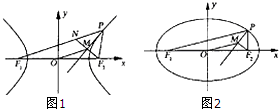 如图,P是双曲线
如图,P是双曲线| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| A、(0,a) |
| B、(0,b) |
| C、(b,a) |
| D、(0,c) |