题目内容
5.已知集合A={x||x-1|≤2},B={x|a<x<a+3},满足A∩B=B,则实数a的取值范围是[-1,0].分析 表示出A中绝对值不等式的解集,根据A与B的交集为B,得到B为A的子集,即可确定出a的范围.
解答 解:A={x||x-1|≤2}={x|-1≤x≤3},B={x|a<x<a+3},
∵A∩B=B,
∴B⊆A,
∴$\left\{\begin{array}{l}{a≥-1}\\{a+3≤3}\end{array}\right.$,
解得-1≤a≤0,
故答案为:[-1,0].
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
16.设A,B,C,D是空间中的四个不同的点,则下列说法错误的是( )
| A. | 若AC与BD共面,则AD与BC也共面 | |
| B. | 若AC与BD是异面直线,则AD与BC也是异面直线 | |
| C. | 若AC与BD是相交直线,则AD与BC也是相交直线 | |
| D. | 若A,B,C,D不共面,则AC与BD既不平行也不相交 |
14.经过同一直线上的3个点的平面( )
| A. | 有且只有一个 | B. | 有且只有3个 | C. | 有无数个 | D. | 不存在 |
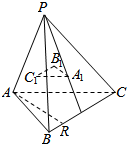 如图,P是△ABC所在平面外的一点,A1,B1,C1依次是△PBC,△PAC,△PAB的重心,AR是平面ABC内的任意一条直线,求证:AR∥平面A1B1C1.
如图,P是△ABC所在平面外的一点,A1,B1,C1依次是△PBC,△PAC,△PAB的重心,AR是平面ABC内的任意一条直线,求证:AR∥平面A1B1C1.