题目内容
设△ABC的外接圆半径为R,且已知AB=4,∠C=45°,则R=分析:根据题意得到边角的关系,进而判断出利用正弦定理求解外接圆的半径.
解答:解:因为在△ABC中AB=4,∠C=45°,
所以根据正弦定理可得:△ABC外接圆的直径2R=
=4
,
所以R=2
.
故答案为2
.
所以根据正弦定理可得:△ABC外接圆的直径2R=
| AB |
| sinC |
| 2 |
所以R=2
| 2 |
故答案为2
| 2 |
点评:本题考查了有关三角形以及外接圆问题,本题主要利用正弦定理解决外接圆的半径问题.

练习册系列答案
相关题目
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤. 选考题
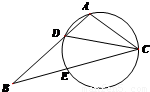
选考题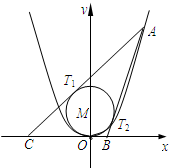 已知A是抛物线
已知A是抛物线 定义域为R,求实数m的取值范围.
定义域为R,求实数m的取值范围. 上的点,点A的坐标为(1,0),O为坐标原点,点M在射线OP上,线段OM与半圆C上的弧AP的长度均为
上的点,点A的坐标为(1,0),O为坐标原点,点M在射线OP上,线段OM与半圆C上的弧AP的长度均为
 上的动点,B、C两点分别在x轴的正、负半轴上,圆M:x2+(y-2)2=4内切于△ABC,切点分别为T1,T2和原点O,设BC=m,AT1=n.
上的动点,B、C两点分别在x轴的正、负半轴上,圆M:x2+(y-2)2=4内切于△ABC,切点分别为T1,T2和原点O,设BC=m,AT1=n. 为定值.
为定值.