题目内容
已知A是抛物线 上的动点,B、C两点分别在x轴的正、负半轴上,圆M:x2+(y-2)2=4内切于△ABC,切点分别为T1,T2和原点O,设BC=m,AT1=n.
上的动点,B、C两点分别在x轴的正、负半轴上,圆M:x2+(y-2)2=4内切于△ABC,切点分别为T1,T2和原点O,设BC=m,AT1=n.(Ⅰ)证明:
 为定值.
为定值.(Ⅱ)已知点A在第一象限,且当△ABC周长最小时,试求△ABC的外接圆方程.

【答案】分析:(Ⅰ)设A(x,y),则 ,所以
,所以 ,由此能证明
,由此能证明 为定值.
为定值.
(Ⅱ)周长l=2(m+n).由 ,知m+n≥16,l≥32,取最小值时,m=n=8,点A
,知m+n≥16,l≥32,取最小值时,m=n=8,点A .
.
设点B的横坐标为x,则直线AB的方程为l: ,点M到l的距离
,点M到l的距离 ,由此及彼能得到所求的方程.
,由此及彼能得到所求的方程.
解答: (本小题满分16分)
(本小题满分16分)
解:(Ⅰ)设A(x,y),则 ,
,
∴ ,∴
,∴ .
.
(Ⅱ)周长l=2(m+n).
∵ ,∴m+n≥16,∴l≥32,
,∴m+n≥16,∴l≥32,
取最小值时,m=n=8,点A的坐标为 .
.
设点B的横坐标为x,则直线AB的方程为l: ,
,
即 .
.
点M到l的距离 ,整理得
,整理得 .
.
故可设所求圆方程为: ,将点
,将点 代入得E=-15,
代入得E=-15,
∴所求的方程为: .
.
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与圆锥曲线的相关知识,解题时要注意合理地进行等价转化.
 ,所以
,所以 ,由此能证明
,由此能证明 为定值.
为定值.(Ⅱ)周长l=2(m+n).由
 ,知m+n≥16,l≥32,取最小值时,m=n=8,点A
,知m+n≥16,l≥32,取最小值时,m=n=8,点A .
.设点B的横坐标为x,则直线AB的方程为l:
 ,点M到l的距离
,点M到l的距离 ,由此及彼能得到所求的方程.
,由此及彼能得到所求的方程.解答:
 (本小题满分16分)
(本小题满分16分)解:(Ⅰ)设A(x,y),则
 ,
,∴
 ,∴
,∴ .
.(Ⅱ)周长l=2(m+n).
∵
 ,∴m+n≥16,∴l≥32,
,∴m+n≥16,∴l≥32,取最小值时,m=n=8,点A的坐标为
 .
.设点B的横坐标为x,则直线AB的方程为l:
 ,
,即
 .
.点M到l的距离
 ,整理得
,整理得 .
.故可设所求圆方程为:
 ,将点
,将点 代入得E=-15,
代入得E=-15,∴所求的方程为:
 .
.点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与圆锥曲线的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
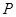 是抛物线
是抛物线 上的动点,点
上的动点,点 轴上的射影是
轴上的射影是 ,点
,点 ,则
,则 的最小值是
( )
的最小值是
( )